
| A. | 5或6 | B. | 6或7 | C. | 7或8 | D. | 以上均错 |
分析 随机变量ξ~B(20,$\frac{1}{3}$),当P(ξ=k)的表达式,由式子的意义知:概率最大也就是ξ最可能的取值.这和期望的意义接近.由Eξ=20×$\frac{1}{3}$=$\frac{20}{3}$,知k=6,或k=7都可能是极值,由此能求出p(ξ=k)取最大值时k的值.
解答 解:随机变量ξ~B(20,$\frac{1}{3}$),
∴当P(ξ=k)=${C}_{20}^{k}$($\frac{1}{3}$)20-k(1-$\frac{1}{3}$)k=($\frac{1}{3}$)20•2k•${C}_{20}^{k}$,
由式子的意义知:概率最大也就是ξ最可能的取值,这和期望的意义接近.
∵Eξ=20×$\frac{1}{3}$=$\frac{20}{3}$,
∴k=6,或k=7都可能是极值,
∵P(ξ=6)=P(ξ=7),
∴p(ξ=k)取最大值时k的值是6或7.
故选:B.
点评 本题考查二项分布的性质和应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 135种 | B. | 90种 | C. | 150种 | D. | 15种 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
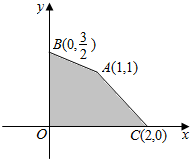 给出平面区域为图中四边形ABOC内部及其边界,目标函数为z=ax-y,若当且仅当x=1,y=1时,目标函数z取最小值,则实数a的取值范围是$-1<a<-\frac{1}{2}$.
给出平面区域为图中四边形ABOC内部及其边界,目标函数为z=ax-y,若当且仅当x=1,y=1时,目标函数z取最小值,则实数a的取值范围是$-1<a<-\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4-2ln2 | D. | 3-2ln2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,0] | B. | (-∞,-2]∪[0,+∞) | C. | [0,2] | D. | (-∞,0]∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com