练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数.

    求不等式的解集；

    若函数的最小值为，整数、满足，求证.

    【答案】(Ⅰ) 或；(Ⅱ)证明见解析.

    【解析】试题分析：（1）根据绝对值定义将不等式转化为三个不等式组，分别求解集，最后求并集（2）根据绝对值三角不等式得，利用均值不等式得， ，即得结果

    试题解析： 当时，得.∴.

    当时，得.∴无解.

    当时，得.

    所以，不等式的解集为或.

    ，∴，即.

    又由均值不等式有： ， ，

    两式相加得.∴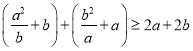

    当且仅当时等号成立.

    点睛:（1）作差法证明不等式，关键在于作差后的变形，一般利用因式分解或配方实现与零的比较，（2）应用基本不等式证明不等式，一要注意方向，二要注意次数统一，三要注意等于号取法（3）反证法证明不等式，基本应用于“正难则反”情形，关键找准矛盾点，推翻反设.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设点，动圆经过点且和直线相切，记动圆的圆心的轨迹为曲线.

    （1）求曲线的方程；

    （2）设曲线上一点的横坐标为，过的直线交于一点，交轴于点，过点作的垂线交于另一点，若是的切线，求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C： =1（a＞b＞0）的左、右焦点分别为F1 ， F2 ， 直线l经过F2且交椭圆C于A，B两点（如图），△ABF1的周长为4 ，原点O到直线l的最大距离为1．

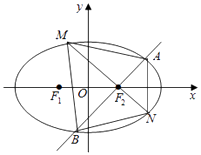
    （1）求椭圆C的标准方程；
    （2）过F2作弦AB的垂线交椭圆C于M，N两点，求四边形AMBN面积最小时直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图四边形ABCD为梯形，AD∥BC，∠ABC=90°，AD=2，AB=4，BC=5，图中阴影部分（梯形剪去一个扇形）绕AB旋转一周形成一个旋转体．
    （1）求该旋转体的表面积；
    （2）求该旋转体的体积．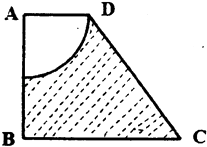

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱ABC﹣A1B1C1中，侧棱AA1⊥底面ABC，AC=3，BC=4，AB=5，AA1=4，点D是AB的中点．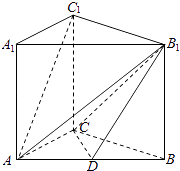

    （1）求证：AC1∥平面CDB1
    （2）求证：AC⊥BC1
    （3）求直线AB1与平面BB1C1C所成的角的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=m（x﹣2m）（x+m+3），g（x）=2x﹣2，若对于任一实数x，f（x）与g（x）至少有一个为负数，则实数m的取值范围是（ ）
    A.（﹣4，﹣1）
    B.（﹣4，0）
    C.（0， ）
    D.（﹣4， ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】交强险是车主必须为机动车购买的险种，若普通6座以下私家车投保交强险第一年的费用（基准保费）统一为元，在下一年续保时，实行的是费率浮动机制，保费与上一年度车辆发生道路交通事故的情况相联系，发生交通事故的次数越多，费率也就越高，具体浮动情况如表：

    交强险浮动因素和浮动费率比率表

    浮动因素

    浮动比率

    上一个年度未发生有责任道路交通事故

    下浮10%

    上两个年度未发生有责任道路交通事故

    下浮20%

    上三个及以上年度未发生有责任道路交通事故

    下浮30%

    上一个年度发生一次有责任不涉及死亡的道路交通事故

    0%

    上一个年度发生两次及两次以上有责任道路交通事故

    上浮10%

    上一个年度发生有责任道路交通死亡事故

    上浮30%

    某机构为了研究某一品牌普通6座以下私家车的投保情况，随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况，统计得到了下面的表格：

    类型

    数量

    10

    5

    5

    20

    15

    5

    以这60辆该品牌车的投保类型的频率代替一辆车投保类型的概率，完成下列问题：

    求一辆普通6座以下私家车（车险已满三年）在下一年续保时保费高于基本保费的频率；

    某二手车销售商专门销售这一品牌的二手车，且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损5000元，一辆非事故车盈利10000元.且各种投保类型车的频率与上述机构调查的频率一致，完成下列问题：

    ①若该销售商购进三辆（车龄已满三年）该品牌二手车，某顾客欲在店内随机挑选两辆车，求这两辆车恰好有一辆为事故车的概率；

    ②若该销售商一次购进120辆（车龄已满三年）该品牌二手车，求一辆车盈利的平均值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共100个，生产一个卫兵需5分钟，生产一个骑兵需7分钟，生产一个伞兵需4分钟，已知总生产时间不超过10小时．若生产一个卫兵可获利润5元，生产一个骑兵可获利润6元，生产一个伞兵可获利润3元．
    （1）用每天生产的卫兵个数x与骑兵个数y表示每天的利润W（元）；
    （2）怎样分配生产任务才能使每天的利润最大，最大利润是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，三棱锥P﹣ABC中，PB⊥底面ABC，∠BCA=90°，PB=BC=CA=2，E为PC的中点，M为AB的中点，点F在PA上，且2PF=FA．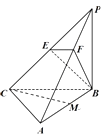

    （1）求证：BE⊥平面PAC；
    （2）求证：CM∥平面BEF；
    （3）求平面ABC与平面BEF所成的二面角的平面角（锐角）的余弦值．

    查看答案和解析>>

    同步练习册答案