
分析 根据题意,(ax+$\frac{1}{x}$)(2x+$\frac{1}{x}$)5展开式中的常数项,是(2x+$\frac{1}{x}$)5的展开式中$\frac{1}{x}$项的系数与ax的系数之积,
再加上x项的系数与$\frac{1}{x}$的系数的积,利用(2x+$\frac{1}{x}$)5展开式的通项公式,求出展开式中含$\frac{1}{x}$与x项的系数,列出方程求出a的值.
解答 解:(ax+$\frac{1}{x}$)(2x+$\frac{1}{x}$)5展开式中的常数项,
是(2x+$\frac{1}{x}$)5的展开式中$\frac{1}{x}$项的系数与ax的系数之积,
再加上x项的系数与$\frac{1}{x}$的系数的积;
又(2x+$\frac{1}{x}$)5展开式的通项公式为:
Tr+1=${C}_{5}^{r}$•(2x)5-r•${(\frac{1}{x})}^{r}$=25-r•${C}_{5}^{r}$•x5-2r,
令5-2r=-1,解得r=3,
∴T3+1=22•${C}_{5}^{3}$•$\frac{1}{x}$=40•$\frac{1}{x}$;
令5-2r=1,解得r=2,
∴T2+1=23•${C}_{5}^{2}$•x=80•x;
∴展开式中的常数项为:
40a+80=-40,
解得a=-3.
故答案为:-3.
点评 本题考查了二项式系数性质的应用问题,熟练掌握二次项系数的性质是解题的关键.


科目:高中数学 来源: 题型:解答题
| 完成时间 | 频率 |
| [20,25) | 0.2 |
| [25,30) | 0.5 |
| [30,35) | 0.2 |
| [35,40) | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{3}$,$\frac{1}{5}$] | B. | [-$\frac{1}{3}$,1] | C. | (-∞,-$\frac{1}{3}$]∪[$\frac{1}{5}$,+∞) | D. | (-∞,-$\frac{1}{3}$]∪[1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
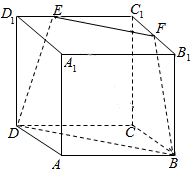 如图,在棱长为6的正方体ABCD-A1B1C1D1中,E,F分别在C1D1与C1B1上,且C1E=4,C1F=3,连接EF,FB,DE,BD,则几何体EFC1-DBC的体积为( )
如图,在棱长为6的正方体ABCD-A1B1C1D1中,E,F分别在C1D1与C1B1上,且C1E=4,C1F=3,连接EF,FB,DE,BD,则几何体EFC1-DBC的体积为( )| A. | 66 | B. | 68 | C. | 70 | D. | 72 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com