
【题目】某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中上学所需时间的范围是![]() ,样本数据分组为
,样本数据分组为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求直方图中x的值;
(2)如果上学所需时间不少于1小时的学生可申请在学校住宿,若该学校有600名新生,请估计新生中有多少名学生可以申请住宿;
(3)由频率分布直方图估计该校新生上学所需时间的平均值.
科目:高中数学 来源: 题型:
【题目】如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点,在五棱锥P﹣ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H. 
(1)求证:AB∥FG;
(2)若PA⊥底面ABCDE,且PA=AE,求直线BC与平面ABF所成角的大小,并求线段PH的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中.已知向量 ![]() 、
、 ![]() ,|
,| ![]() |=|
|=| ![]() |=1,
|=1, ![]()
![]() =0,点Q满足
=0,点Q满足 ![]() =
= ![]() (
( ![]() +
+ ![]() ),曲线C={P|
),曲线C={P| ![]() =
= ![]() cosθ+
cosθ+ ![]() sinθ,0≤θ≤2π},区域Ω={P|0<r≤|
sinθ,0≤θ≤2π},区域Ω={P|0<r≤| ![]() |≤R,r<R}.若C∩Ω为两段分离的曲线,则( )
|≤R,r<R}.若C∩Ω为两段分离的曲线,则( )
A.1<r<R<3
B.1<r<3≤R
C.r≤1<R<3
D.1<r<3<R
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机调查![]() 名性别不同的大学生是否喜欢打羽毛球,得到如下
名性别不同的大学生是否喜欢打羽毛球,得到如下![]() 列联表:
列联表:
男 | 女 | 总计 | |
喜欢打羽毛球 |
|
|
|
不喜欢打羽毛球 |
|
|
|
总计 |
|
|
|
临界值表:
|
|
|
|
|
|
|
|
参考公式:![]() (其中
(其中![]() )
)
参照临界值表,下列结论正确的是( )
A. 在犯错误的概率不超过![]() 的前提下,认为“喜欢打羽毛球与性别有关”
的前提下,认为“喜欢打羽毛球与性别有关”
B. 在犯错误的概率不超过![]() 的前提下,认为“喜欢打羽毛球与性别无关”
的前提下,认为“喜欢打羽毛球与性别无关”
C. 在犯错误的概率不超过![]() 的前提下,认为“喜欢打羽毛球与性别有关”
的前提下,认为“喜欢打羽毛球与性别有关”
D. 在犯错误的概率不超过![]() 的前提下,认为“喜欢打羽毛球与性别无关”
的前提下,认为“喜欢打羽毛球与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取m个作为样本,称出它们的重量(单位:克),重量分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,由此得到样本的重量频率分布直方图(如图).
,由此得到样本的重量频率分布直方图(如图).
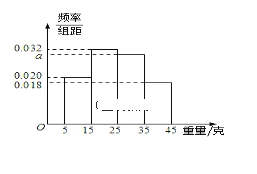
(1)根据样本数据,试估计盒子中小球重量的中位数与平均值(精确到0.01);
(2)从盒子装的大量小球中,随机抽取3个小球,其中重量在![]() 内的小球个数为
内的小球个数为![]() ,求
,求![]() 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com