
 Ϊ�������������������ij��������һ���Լ400m��400m�Ľӽ������λĵ��Ͻ�һ��������㳡������Ҫ������ͼ��ʾ��һ�������Ϊ4000m2�ľ��γ��أ�������Ӱ����Ϊͨ����ͨ�����Ⱦ�Ϊ2�ף��м�������������������ܽ�������Ϊ�����˶����أ���������С������״��ͬ����������ƾ��γ��صij��Ϳ���ʹ�ܽ��˶�����ռ��������������ֵ��
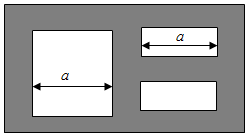
Ϊ�������������������ij��������һ���Լ400m��400m�Ľӽ������λĵ��Ͻ�һ��������㳡������Ҫ������ͼ��ʾ��һ�������Ϊ4000m2�ľ��γ��أ�������Ӱ����Ϊͨ����ͨ�����Ⱦ�Ϊ2�ף��м�������������������ܽ�������Ϊ�����˶����أ���������С������״��ͬ����������ƾ��γ��صij��Ϳ���ʹ�ܽ��˶�����ռ��������������ֵ�� ���� ����γ��صij�Ϊxm����Ϊym���ܽ��˶�����ռ�������ΪSm2�������Ϊxy=4000����2a+6=x��a=$\frac{x-6}{2}$��y=$\frac{4000}{x}$���Ӷ��˶���ռ�����ΪS=��y-4��a+��y-6��a=��2y-10��a=��x-6����$\frac{4000}{x}$-5������a��0���ɵ�x��6��$\frac{4000}{x}$-5��0���ɵ�x��800���䶨�����ǣ�6��800������S=4030-��5x+$\frac{24000}{x}$�����ɻ�������ʽ�ɵú��������ֵ���Լ���Ӧ��x��y��ֵ��
��� �⣺����γ��صij�Ϊxm����Ϊym���ܽ��˶�����ռ�������ΪSm2��
����xy=4000��y=$\frac{4000}{x}$��
S=��y-4��a+��y-6��a=��2y-10��a��
��2a+6=x���ɵ�a=$\frac{x-6}{2}$��S=��$\frac{8000}{x}$-10��•$\frac{x-6}{2}$=��x-6����$\frac{4000}{x}$-5����
��a��0���ɵ�x��6��$\frac{4000}{x}$-5��0���ɵ�x��800��
�䶨�����ǣ�6��800����
��S=4030-��5x+$\frac{24000}{x}$����4030-2$\sqrt{5x•\frac{24000}{x}}$=4030-400$\sqrt{3}$��
���ҽ���5x=$\frac{24000}{x}$����x=40$\sqrt{3}$�ʣ�6��800��ʱ����������ʽ�Ⱥų�����
��ʱx=40$\sqrt{3}$��y=$\frac{100\sqrt{3}}{3}$��Smax=4030-400$\sqrt{3}$��
�����x=40$\sqrt{3}$m��y=$\frac{100\sqrt{3}}{3}$mʱ���˶��������������ֵΪ4030-400$\sqrt{3}$ƽ����
���� ������ʵ������Ϊ���壬���麯��ģ�͵Ĺ���������Ӧ�û�������ʽ������ֵ������������ϵʽ�ǹؼ��������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b��c | B�� | c��a��b | C�� | c��b��a | D�� | b��c��a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
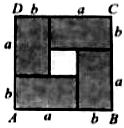 ��ͼ��ʾ����С���εij�������Ϊa��b���ְ��ĸ�ͬ���ľ���ƴ�ӳ������κ���������Ӱ���־������֮�������������֮��Ĺ�ϵ�����ò���ʽ���������
��ͼ��ʾ����С���εij�������Ϊa��b���ְ��ĸ�ͬ���ľ���ƴ�ӳ������κ���������Ӱ���־������֮�������������֮��Ĺ�ϵ�����ò���ʽ����������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com