
| A. | a<b<c | B. | c<a<b | C. | c<b<a | D. | b<c<a |
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {-1,1,2} | C. | {-2,-1} | D. | {-2,-1,0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18 | B. | 2 | C. | 2$\sqrt{3}$ | D. | 2$\root{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
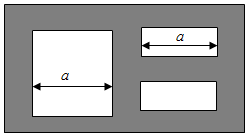 为了满足社区居民健身活动,某社区准备在一块大约400m×400m的接近正方形荒地上建一个健身活动广场,首先要建设如图所示的一个总面积为4000m2的矩形场地,其中阴影部分为通道,通道宽度均为2米,中间的三个矩形区域将铺设塑胶地面作为健身运动场地(其中两个小场地形状相同),怎样设计矩形场地的长和宽,使塑胶运动场地占地面积最大,并求出最大值.
为了满足社区居民健身活动,某社区准备在一块大约400m×400m的接近正方形荒地上建一个健身活动广场,首先要建设如图所示的一个总面积为4000m2的矩形场地,其中阴影部分为通道,通道宽度均为2米,中间的三个矩形区域将铺设塑胶地面作为健身运动场地(其中两个小场地形状相同),怎样设计矩形场地的长和宽,使塑胶运动场地占地面积最大,并求出最大值.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
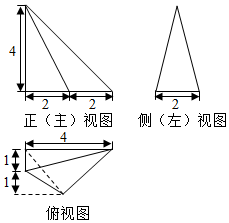
| A. | 2$\sqrt{2}$ | B. | $\sqrt{17}$ | C. | 3$\sqrt{2}$ | D. | $\sqrt{33}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com