
分析 (1)根据两个椭圆有相同的离心率,利用待定系数法进行求解即可.
(2)利用待定系数法,结合条件求出a,b的值即可得到结论.
解答 解:(1)∵焦点在x轴上,与椭圆$\frac{x^2}{4}$+$\frac{y^2}{3}$=1具有相同的离心率,
∴设对应的椭圆方程为$\frac{x^2}{4}$+$\frac{y^2}{3}$=λ,(λ>0),
∵椭圆过点(2,-$\sqrt{3}$),
∴λ=$\frac{4}{4}+\frac{3}{3}=1+1=2$,
即对应的椭圆方程为$\frac{x^2}{4}$+$\frac{y^2}{3}$=2,
即$\frac{x^2}{8}+\frac{y^2}{6}=1$.
(2)当焦点在x轴上时,设所求双曲线的方程为$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1,
∵顶点间的距离为6,渐近线方程为y=±$\frac{1}{3}$x,
∴$\left\{\begin{array}{l}2a=6\\ \frac{b}{a}=\frac{1}{3}.\end{array}\right.$解得a=3,b=1.
则焦点在x轴上的双曲线的方程为$\frac{x^2}{9}-{y^2}=1$.
点评 本题主要考查椭圆和双曲线方程的求解,利用待定系数法是解决本题的关键.比较基础.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,使得ex0≤0 | B. | sinx+$\frac{1}{sinx}$≥2(x≠kπ,k∈Z) | ||
| C. | ?x∈R,2x>x2 | D. | a>1,b>1是ab>1的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
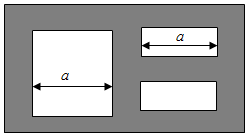 为了满足社区居民健身活动,某社区准备在一块大约400m×400m的接近正方形荒地上建一个健身活动广场,首先要建设如图所示的一个总面积为4000m2的矩形场地,其中阴影部分为通道,通道宽度均为2米,中间的三个矩形区域将铺设塑胶地面作为健身运动场地(其中两个小场地形状相同),怎样设计矩形场地的长和宽,使塑胶运动场地占地面积最大,并求出最大值.
为了满足社区居民健身活动,某社区准备在一块大约400m×400m的接近正方形荒地上建一个健身活动广场,首先要建设如图所示的一个总面积为4000m2的矩形场地,其中阴影部分为通道,通道宽度均为2米,中间的三个矩形区域将铺设塑胶地面作为健身运动场地(其中两个小场地形状相同),怎样设计矩形场地的长和宽,使塑胶运动场地占地面积最大,并求出最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com