
分析 ( I)利用基底的定义可知:a,b互质可以作为一个基底.
( II)m以(a,b)为基底的坐标(x,y)有无数个.若(a,b)为基底,对于?的整数m,?x0,y0∈Z,使m=x0a+y0b成立,可得(x0+kb,y0-kb),k∈Z,都是数m以(a,b)为基底的坐标.利用等腰证明即可.
( III)m=2k+1,k∈N*,理由如下:首先,对任意m=2k,k∈N*,(2,m)不是全体整数的一个基底;利用反证法即可证明.利用定义即可证明,对所有满足题意的正奇数,对任意m=2k+1,k∈N*,(2,2k+1)是全体整数的一个基底.
解答 解:( I)利用基底的定义可知:a,b互质可以作为一个基底,因此(2,3),(2,5),(3,5),(9,17)符合条件.
( II)m以(a,b)为基底的坐标(x,y)有无数个.
∵(a,b)为基底,对于?的整数m,?x0,y0∈Z,使m=x0a+y0b成立,
即(x0,y0)为数m以(a,b)为基底的坐标,则(x0+kb,y0-kb),k∈Z,都是数m以(a,b)为基底的坐标,
证明如下:(x0+kb)a+(y0-ka)b=x0a+y0b+kba-kba=m,
∴(x0+kb,y0-ka),k∈Z,都是数m以(a,b)为基底的坐标,有无数个.
( III)m=2k+1,k∈N*,理由如下:
首先,对任意m=2k,k∈N*,(2,m)不是全体整数的一个基底;反证法,
假设此时(2,m)是全体整数的一个基底,则?x,y∈Z,有1=2x+my成立,
而数2,m都为偶数,所以2x+my为偶数,不可能等于1,所以假设不成立,即对任意m=2k,k∈N*,(2,m)不是全体整数的一个基底.
下面证明,对所有满足题意的正奇数,对任意m=2k+1,k∈N*,(2,2k+1)是全体整数的一个基底.
∵1=-k×2+1×(2k+1),即(-k,1)为数1以(2,2k+1)为基底的坐标,对于?m∈Z,显然(-km,m)为数m以(2,2k+1)为基底的坐标,即?-km,m∈Z,使m=-km×2+m×(2k+1)成立,即对任意m=2k+1,k∈N*,(2,2k+1)是全体整数的一个基底.
点评 本题考查了新定义数对基底、反证法,考查了分析问题与解决问题的能力、推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
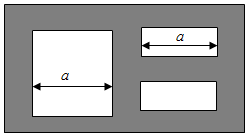 为了满足社区居民健身活动,某社区准备在一块大约400m×400m的接近正方形荒地上建一个健身活动广场,首先要建设如图所示的一个总面积为4000m2的矩形场地,其中阴影部分为通道,通道宽度均为2米,中间的三个矩形区域将铺设塑胶地面作为健身运动场地(其中两个小场地形状相同),怎样设计矩形场地的长和宽,使塑胶运动场地占地面积最大,并求出最大值.
为了满足社区居民健身活动,某社区准备在一块大约400m×400m的接近正方形荒地上建一个健身活动广场,首先要建设如图所示的一个总面积为4000m2的矩形场地,其中阴影部分为通道,通道宽度均为2米,中间的三个矩形区域将铺设塑胶地面作为健身运动场地(其中两个小场地形状相同),怎样设计矩形场地的长和宽,使塑胶运动场地占地面积最大,并求出最大值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
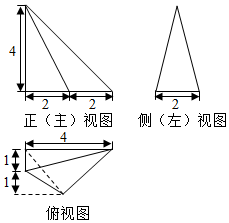
| A. | 2$\sqrt{2}$ | B. | $\sqrt{17}$ | C. | 3$\sqrt{2}$ | D. | $\sqrt{33}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}\sqrt{6}$ | B. | $\frac{3}{5}\sqrt{6}$ | C. | $\frac{4}{5}\sqrt{6}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 1 | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com