
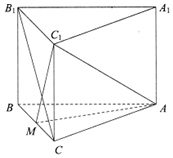
 在三棱柱ABC-A1B1C1中,已知侧棱CC1⊥底面ABC,M为BC的中点,$AC=AB=3,BC=2,C{C_1}=\sqrt{2}$.
在三棱柱ABC-A1B1C1中,已知侧棱CC1⊥底面ABC,M为BC的中点,$AC=AB=3,BC=2,C{C_1}=\sqrt{2}$.分析 (1)证明CC1⊥AM,经过计算推出MC1⊥B1C,结合AM⊥B1C,即可证明B1C⊥平面AMC1.
(2)设点A1到平面AMC1的距离为h,利用${V_{{A_1}-AMC}}={V_{{C_1}-AMC}}$,推出$\frac{1}{3}{S_{△AM{C_1}}}•h=\frac{1}{3}{S_{△AMC}}•C{C_1}$,然后求解点A1到平面AMC1的距离.
解答 解:(1)证明:在△ABC中,AC=AB,M为BC的中点,
故AM⊥BC,又侧棱CC1⊥底面ABC,所以CC1⊥AM,
又BC∩CC1=C,所以AM⊥平面BCC1B1,
则AM⊥B1C,在Rt△BCB1中,$tan∠{B_1}CB=\frac{{{B_1}B}}{BC}=\frac{{\sqrt{2}}}{2}$;在Rt△MCC1中,$tan∠M{C_1}C=\frac{MC}{{{C_1}C}}=\frac{1}{{\sqrt{2}}}=\frac{{\sqrt{2}}}{2}$,所以∠B1CB=∠MC1C,
又∠B1CB+∠C1CB1=90°,所以∠MC1C+∠C1CB1=90°,
即MC1⊥B1C,又AM⊥B1C,AM∩MC1=M,所以B1C⊥平面AMC1.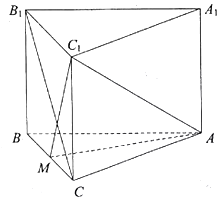
(2)设点A1到平面AMC1的距离为h,由于${V_{{A_1}-AM{C_1}}}={V_{M-{A_1}A{C_1}}}={V_{{C_1}-AMC}}$,
∴${V_{{A_1}-AMC}}={V_{{C_1}-AMC}}$,即$\frac{1}{3}{S_{△AM{C_1}}}•h=\frac{1}{3}{S_{△AMC}}•C{C_1}$,于是$h=\frac{{{S_{△AMC}}•C{C_1}}}{{{S_{△AM{C_1}}}}}=\frac{{\frac{1}{2}•AM•MC•C{C_1}}}{{\frac{1}{2}•AM•{C_1}M}}=\frac{{MC•C{C_1}}}{{{C_1}M}}=\frac{{\sqrt{2}}}{{\sqrt{3}}}=\frac{{\sqrt{6}}}{3}$,
所以点A1到平面AMC1的距离为$\frac{{\sqrt{6}}}{3}$.
点评 本题考查直线与平面垂直的判定定理的应用,等体积法的应用,点到平面的距离的求法,考查空间想象能力以及计算能力.


科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 18 | C. | 24 | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [3,+∞) | B. | (3,+∞) | C. | (-∞,-1) | D. | (1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{5}$ | B. | $8\sqrt{5}$ | C. | $4\sqrt{15}$ | D. | $8\sqrt{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{{\sqrt{3}}}{6},\frac{{\sqrt{3}}}{4}]$ | B. | $(\frac{{\sqrt{3}}}{6},\frac{{\sqrt{3}}}{4})$ | C. | $(\frac{{\sqrt{3}}}{12},\frac{{\sqrt{3}}}{4})$ | D. | $(\frac{{\sqrt{3}}}{12},\frac{{\sqrt{3}}}{4}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{kπ-\frac{π}{3},kπ+\frac{π}{6}}]$,(k∈Z) | B. | $[{kπ-\frac{π}{12},kπ+\frac{5π}{12}}]$,(k∈Z) | ||
| C. | $[{kπ-\frac{7π}{12},kπ-\frac{π}{12}}]$,(k∈Z) | D. | $[{kπ+\frac{π}{6},kπ+\frac{2π}{3}}]$,(k∈Z) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com