
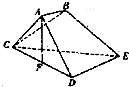
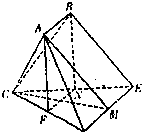
 已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2a,AB=a,F为CD的中点.
已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2a,AB=a,F为CD的中点.
|
|
| ||
| 5 |
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
|


科目:高中数学 来源: 题型:
| S1+S2+…+Sn |
| n |
| A、23 | B、24 | C、22 | D、20 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 9 |
| y2 |
| 4 |
| A、4 | B、5 | C、6 | D、9 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 2 |
A、[-
| ||||
B、[-
| ||||
C、(-∞,-
| ||||
D、[
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在智利地震灾区的搜救现场,一条搜救狗沿正北方向行进xm发现生命迹象,然后向右转105°,行进10m发现另一生命迹象,这时它向右转135°后续继前行回到出发点,那么x=
如图,在智利地震灾区的搜救现场,一条搜救狗沿正北方向行进xm发现生命迹象,然后向右转105°,行进10m发现另一生命迹象,这时它向右转135°后续继前行回到出发点,那么x=查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com