
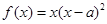 ,
,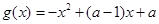 (其中
(其中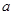 为常数).
为常数).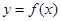 和
和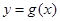 有相同的极值点,求
有相同的极值点,求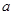 的值;
的值;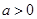 ,问是否存在
,问是否存在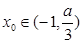 ,使得
,使得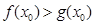 ,若存在,请求出实数
,若存在,请求出实数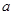 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.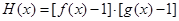 ,若函数
,若函数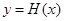 有5个不同的零点,求实数
有5个不同的零点,求实数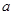 的取值范围.
的取值范围. 或
或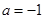 ;(2)
;(2)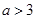 ;(3)
;(3) .
.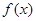 求导,得到
求导,得到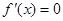 有2个根,而
有2个根,而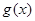 在
在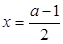 处有极大值,所以那2个根分别等于
处有极大值,所以那2个根分别等于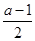 ,得到a的值;第二问,假设存在
,得到a的值;第二问,假设存在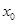 使得
使得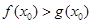 ,将
,将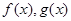 代入得到解析式,由于
代入得到解析式,由于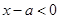 ,所以将问题转化成了存在
,所以将问题转化成了存在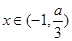 ,使得
,使得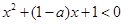 ,分类讨论,讨论抛物线的对称轴和区间端点的大小,数形结合,得到结论;第三问,已知条件中
,分类讨论,讨论抛物线的对称轴和区间端点的大小,数形结合,得到结论;第三问,已知条件中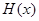 有5个不同的零点,根据
有5个不同的零点,根据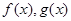 解析式的特点,知
解析式的特点,知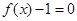 有3个不同的实根,
有3个不同的实根,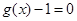 有2个不同的实根,通过抛物线的图形可知要使
有2个不同的实根,通过抛物线的图形可知要使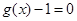 有2个不同的实根,只需
有2个不同的实根,只需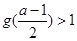 ,而
,而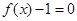 ,通过第一问得到的极值点,讨论2个数的3种大小关系,结合图象,确定a的取值范围,a的取值范围需保证
,通过第一问得到的极值点,讨论2个数的3种大小关系,结合图象,确定a的取值范围,a的取值范围需保证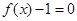 和
和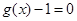 同时成立,还得保证这5个根互不相等.
同时成立,还得保证这5个根互不相等.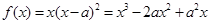 ,则
,则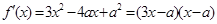 ,
,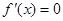 ,得
,得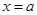 或
或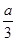 ,而
,而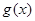 在
在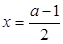 处有极大值,
处有极大值, 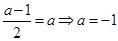 或
或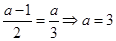 ;综上:
;综上: 或
或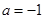 . 3分
. 3分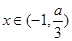 ,使得
,使得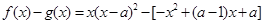
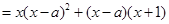
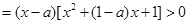 ,
,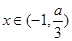 时,又
时,又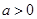 ,故
,故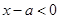 ,则存在
,则存在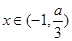 ,使得
,使得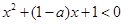 , 4分
, 4分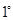 当
当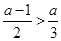 即
即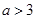 时,
时,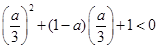 得
得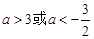 ,
,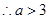 ;
; 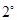 当
当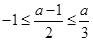 即
即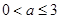 时,
时,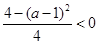 得
得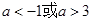 , 6分
, 6分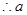 无解;综上:
无解;综上: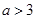 . 7分
. 7分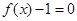 有3个不同的实根,
有3个不同的实根,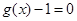 有2个不同的实根,且这5个实根两两不相等.\(ⅰ)
有2个不同的实根,且这5个实根两两不相等.\(ⅰ)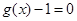 有2个不同的实根,只需满足
有2个不同的实根,只需满足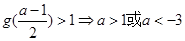 ; 8分
; 8分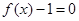 有3个不同的实根,
有3个不同的实根,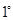 当
当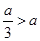 即
即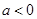 时,
时,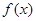 在
在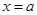 处取得极大值,而
处取得极大值,而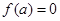 ,不符合题意,舍; 9分
,不符合题意,舍; 9分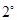 当
当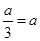 即
即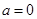 时,不符合题意,舍;
时,不符合题意,舍;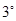 当
当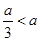 即
即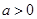 时,
时,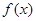 在
在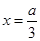 处取得极大值,
处取得极大值,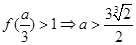 ;所以
;所以 ; 10分
; 10分 ;(注:
;(注: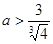 也对) 11分
也对) 11分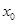 使得
使得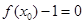 和
和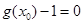 同时成立.
同时成立.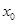 使得
使得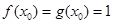 ,
,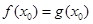 ,即
,即 ,得
,得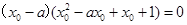 ,
,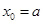 时,
时,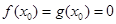 ,不符合,舍去;
,不符合,舍去;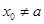 时,既有
时,既有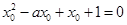 ①;
①;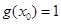 ,即
,即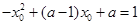 ②; 联立①②式,可得
②; 联立①②式,可得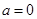 ;
;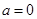 时,
时,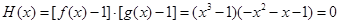 没有5个不
没有5个不 时,函数
时,函数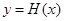 有5个不同的零点. 14分
有5个不同的零点. 14分

 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源:不详 题型:解答题
 ,
, 的单调区间;
的单调区间; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;  的方程
的方程 在区间
在区间 上恰好有两个相异的实根,求实数
上恰好有两个相异的实根,求实数 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
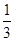 x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)的图象,则f(-1)等于( )
x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)的图象,则f(-1)等于( )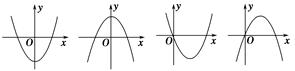
A.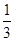 | B.-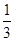 | C.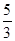 | D.-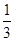 或 或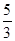 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.(-1,1) |
| B.(-1,+∞) |
| C.(-∞,-1) |
| D.(-∞,+∞) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
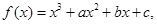 下列结论中①
下列结论中①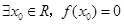 ②函数
②函数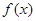 的图象是中心对称图形 ③若
的图象是中心对称图形 ③若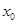 是
是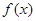 的极小值点,则
的极小值点,则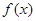 在区间
在区间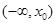 单调递减 ④若
单调递减 ④若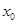 是
是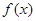 的极值点,则
的极值点,则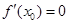 . 正确的个数有( )
. 正确的个数有( )| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com