Question

5．如图，四边形ABCD中，AB⊥AD，AD∥BC，AD=6，BC=2AB=4，E，F分别在BC，AD上，EF∥AB，现将四边形ABCD沿EF折起，使平面ABEF⊥平面EFDC．
（1）若BE=1，是否在折叠后的线段AD上存在一点P，且$\overrightarrow{AP}$=λ$\overrightarrow{PD}$，使得CP∥平面ABEF？若存在，求出λ的值，若不存在，说明理由；
（2）求三棱锥A-CDF的体积的最大值，并求出此时二面角E-AC-F的余弦值．

Answer 1

分析 （1）由EF∥AB，AB⊥AD，可得EF⊥AF，EF⊥FD，折起后平面ABEF⊥平面EFDC，可得AF⊥平面EFDC．假设线段AD上存在一点P，且$\overrightarrow{AP}$=λ$\overrightarrow{PD}$，使得CP∥平面ABEF．若BE=1，可得平面ABEF的法向量为$\overrightarrow{FD}$=（0，5，0）．由$\overrightarrow{AP}$=λ$\overrightarrow{PD}$，可得$\overrightarrow{FP}=\frac{1}{1+λ}\overrightarrow{FA}+\frac{λ}{1+λ}\overrightarrow{FD}$，可得$\overrightarrow{CP}$，利用$\overrightarrow{CP}•\overrightarrow{FD}$，解得λ即可判断出．
（2）设BE=a，可得AF=a（0＜a≤4），FD=6-a．V_{三棱锥A-CFD}=$\frac{1}{3}×a×\frac{1}{2}×2×（6-a）$，利用基本不等式的性质可得：当且仅当a=3时取等号．三棱锥A-CDF的体积有最大值．设平面ACE的法向量为$\overrightarrow{m}$=（x₁，y₁，z₁），利用$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AC}=0}\\{\overrightarrow{m}•\overrightarrow{AE}=0}\end{array}\right.$，可得$\overrightarrow{m}$．设平面ACF的法向量为$\overrightarrow{n}$，同理可得$\overrightarrow{n}$，利用$cos＜\overrightarrow{m}，\overrightarrow{n}＞$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$即可得出．

解答 解：（1）∵EF∥AB，AB⊥AD，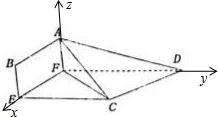
∴EF⊥AF，EF⊥FD，
折起后平面ABEF⊥平面EFDC．平面ABEF∩平面EFDC=EF．
∴AF⊥平面EFDC．
假设线段AD上存在一点P，且$\overrightarrow{AP}$=λ$\overrightarrow{PD}$，使得CP∥平面ABEF．
∵BE=1，可得F（0，0，0），A（0，0，1），D（0，5，0），C（2，3，0）．
可得平面ABEF的法向量为$\overrightarrow{FD}$=（0，5，0）．
∵$\overrightarrow{AP}$=λ$\overrightarrow{PD}$，∴$\overrightarrow{FP}=\frac{1}{1+λ}\overrightarrow{FA}+\frac{λ}{1+λ}\overrightarrow{FD}$=$\frac{1}{1+λ}（0，0，1）$+$\frac{λ}{1+λ}（0，5，0）$=$（0，\frac{5λ}{1+λ}，\frac{1}{1+λ}）$，
∴P$（0，\frac{5λ}{1+λ}，\frac{1}{1+λ}）$，
∴$\overrightarrow{CP}$=$（-2，\frac{2λ-3}{1+λ}，\frac{1}{1+λ}）$，则$\overrightarrow{CP}•\overrightarrow{FD}$=$\frac{5（2λ-3）}{1+λ}=0$，解得$λ=\frac{3}{2}$．
∴线段AD上存在一点P$（0，3，\frac{2}{5}）$，且$\overrightarrow{AP}$=$\frac{3}{2}$$\overrightarrow{PD}$，使得CP∥平面ABEF．
（2）设BE=a，∴AF=a（0＜a≤4），FD=6-a．
∴V_{三棱锥A-CFD}=$\frac{1}{3}×a×\frac{1}{2}×2×（6-a）$=$\frac{1}{3}a（6-a）$$≤\frac{1}{3}×（\frac{a+6-a}{2}）^{2}$=3，当且仅当a=3时取等号．
∴当a=3时，三棱锥A-CDF的体积有最大值3．
可得A（0，0，3），D（0，3，0），C（2，1，0），E（2，0，0），
∴$\overrightarrow{AE}$=（2，0，-3），$\overrightarrow{AC}$=（2，1，-3），$\overrightarrow{FA}$=（0，0，3），$\overrightarrow{FC}$=（2，1，0）．
设平面ACE的法向量为$\overrightarrow{m}$=（x₁，y₁，z₁），则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AC}=0}\\{\overrightarrow{m}•\overrightarrow{AE}=0}\end{array}\right.$，
∴$\left\{\begin{array}{l}{2{x}_{1}+{y}_{1}-3{z}_{1}=0}\\{2{x}_{1}-3{z}_{1}=0}\end{array}\right.$，令x₁=3，解得y₁=0，z₁=2，
∴$\overrightarrow{m}$=（3，0，2）．
设平面ACF的法向量为$\overrightarrow{n}$=（x₂，y₂，z₂），则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{FA}=0}\\{\overrightarrow{n}•\overrightarrow{FC}=0}\end{array}\right.$，
同理可得$\overrightarrow{n}$=（1，-2，0），
∴$cos＜\overrightarrow{m}，\overrightarrow{n}＞$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{3}{\sqrt{13}×\sqrt{5}}$=$\frac{3\sqrt{65}}{65}$，
∴二面角E-AC-F的余弦值为$\frac{3\sqrt{65}}{65}$．

点评 本题考查了线面平行与垂直的判定与性质定理，考查了通过建立空间直角坐标系利用向量垂直与数量积的关系及平面的法向量的夹角求出二面角的方法，考查了空间想象能力，考查了推理能力与计算能力，属于中档题．