Question

7．在等腰直角△ABC中，AB=AC=4，点P是边AB上异于A、B的一点，光线从点P出发经过BC、CA反射后又回到点P，光线交线段BC于点Q，交线段CA于点R，若光线QR经过△ABC的重心，求线段AP的长度．

Answer 1

分析 建立坐标系，可得直线方程和重心坐标，由反射原理可得P的两个对称点坐标，可得直线方程，进而可得P的坐标，可得AP长度．

解答 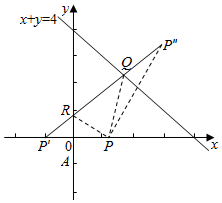解：由题意建立如图所示的坐标系，则A（0，0），B（4，0），C（0，4），可得BC的方程为x+y=4，可得重心（$\frac{4}{3}$，$\frac{4}{3}$）
设P（a，0），则P关于AC即y轴的对称点P′（-a，0），
设P关于BC的对称点P″（m，n），则$\left\{\begin{array}{l}{\frac{m+a}{2}+\frac{n+0}{2}=4}\\{\frac{n-0}{m-a}•（-1）=-1}\end{array}\right.$，
解得$\left\{\begin{array}{l}{m=4}\\{n=4-a}\end{array}\right.$，即P″（4，4-a），
∴光线QR即P′P″的方程为y=$\frac{4-a}{4+a}$（x+a），
代入（$\frac{4}{3}$，$\frac{4}{3}$）可得$\frac{4}{3}$=$\frac{4-a}{4+a}$（$\frac{4}{3}$+a），
解得a=$\frac{4}{3}$或a=0（舍去）
∴线段AP的长度为$\frac{4}{3}$

点评 本题考查直线和点的对称性，涉及光的反射原理和方程组的解法，属中档题．