练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】若直线经过 两点，则直线 的倾斜角为( )
    A.30°
    B.45°
    C.60°
    D.120°

    【答案】C
    【解析】解答：设直线 的倾斜角为， 直线经过 两点，所以 ，即 ，又因为 ，所以 . 分析：本题主要考查了直线的倾斜角、直线的斜率、斜率的计算公式，解决问题的关键是根据直线倾斜角与斜率的关系进行计算即可.
    【考点精析】掌握直线的倾斜角和直线的斜率是解答本题的根本，需要知道当直线l与x轴相交时, 取x轴作为基准, x轴正向与直线l向上方向之间所成的角α叫做直线l的倾斜角.特别地,当直线l与x轴平行或重合时, 规定α=0°；一条直线的倾斜角α(α≠90°)的正切值叫做这条直线的斜率,斜率常用小写字母k表示,也就是 k = tanα．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某小区一住户在楼顶违规私自建了“阳光房”，该小区其他居民对此意见很大，通过物业和城管部门多次上门协调，该住户终于拆除了“阳光房”，对此有人认为既然已经建成再拆除太可惜了，为此业主委员会通过随机询问小区100名性别不同的居民对此件事情的看法，得到如下的2×2列联表

    认为应该拆除

    认为太可惜了

    总计

    男

    45

    10

    55

    女

    30

    15

    45

    总计

    75

    25

    100

    附：

    P（K2≥k）

    0.10

    0.05

    0.025

    k

    2.706

    3.841

    5.024

    K2= ，其中n=a+b+c+d
    参照附表，由此可知下列选项正确的是（ ）
    A.在犯错误的概率不超过1%的前提下，认为“是否认为拆除太可惜了与性别有关”
    B.在犯错误的概率不超过1%的前提下，认为“是否认为拆除太可惜了与性别无关”
    C.有90%以上的把握认为“是否认为拆除太可惜了与性别有关”
    D.有90%以上的把握认为“是否认为拆除太可惜了与性别无关”

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】近年来我国电子商务行业迎来蓬勃发展的新机遇，网购成了大众购物的一个重要组成部分，可人们在开心购物的同时，假冒伪劣产品也在各大购物网站频频出现，为了让顾客能够在网上买到货真价实的好东西，各大购物平台也推出了对商品和服务的评价体系，现从某购物网站的评价系统中选出100次成功的交易，并对其评价进行统计，对商品的好评率为 ，对服务的好评率为 ，其中对商品和服务都做出好评的交易为30次．
    （1）列出关于商品和服务评价的2×2列联表，并判断是否可以在犯错误概率不超过1%的前提下，认为商品好评与服务好评有关？
    （2）若针对商品的好评率，采用分层抽样的方式从这100次交易中取出5次交易，并从中选择两次交易进行客户回访，求只有一次好评的概率．

    P（K2≥k）

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    k

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    （K2= ，其中n=a+b+c+d）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知平行四边形 的三个顶点的坐标为 ， ， ．
    （1）在 ABC中，求边AC中线所在直线方程；
    （2）求平行四边形 的顶点D的坐标及边BC的长度;
    （3）求 的面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x+ ，g（x）=2x+a，若x1∈[ ，3]，x2∈[2，3]，使得f（x1）≥g（x2），则实数a的取值范围是（ ）
    A.a≤1
    B.a≥1
    C.a≤0
    D.a≥0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】学校为了解学生的数学学习情况，在全校高一年级学生中进行了抽样调查，调查结果如表所示：

    喜欢数学

    不喜欢数学

    合计

    男生

    60

    20

    80

    女生

    10

    10

    20

    合计

    70

    30

    100


    （1）根据表中数据，问是否有95%的把握认为“男生和女生在喜欢数学方面有差异”；
    （2）在被调查的女生中抽出5名，其中2名喜欢数学，现在从这5名学生中随机抽取3人，求至多有1人喜欢数学的概率．
    附：参考公式：K2= ，其中n=a+b+c+d

    P（K2≥k）

    0.100

    0.050

    0.010

    k

    2.706

    3.841

    6.635

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，正三角形ABC的边BC所在直线斜率是0,则AC、AB所在的直线斜率之和为（ ）
    A.-
    B.0
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，ABCD﹣A1B1C1D1为正方体，下面结论错误的序号是 ．
    ①BD∥平面CB1D1；
    ②AC1⊥BD；
    ③AC1⊥平面CB1D1；
    ④异面直线AD与CB1所成角为60°．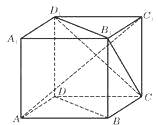

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆： 经过点，左右焦点分别为、，圆与直线相交所得弦长为2．　

    （Ⅰ）求椭圆的标准方程；

    （Ⅱ）设是椭圆上不在轴上的一个动点， 为坐标原点，过点作的平行线交椭圆于、两个不同的点，求的取值范围．

    查看答案和解析>>

    同步练习册答案