已知函数f(x)=ax3+bx2-9x在x=3处取得极大值0.
(Ⅰ)求f(x)在区间[0,1]上的最大值;
(Ⅱ)若过点P(-1,m)可作曲线y=f(x)的切线有三条,求实数m的取值范围.
解:(Ⅰ)∵f′(x)=3ax
2+2bx-9,
且在x=3处取得极大值0.
∴
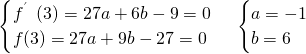
∴f′(x)=-3x
2+12x-9=-3(x-1)(x-3)
当x∈[0,1]时,f′(x)≤0,
∴f(x)在[0,1]上单调递减.
∴f
max(x)=f(0)=0.…(6分)
(Ⅱ)设过P点的切线切曲线于点(x
0,y
0),则切线的斜率k=-3x
02+12x
0-9
所以切线方程为y=(-3x
02+12x
0-9)(x+1)+mw
故y
0=(-3x
02+12x
0-9)(x
0+1)+m=-x
03+6x
02-9x
0…(9分)
要使过P可作曲线y=f(x)的切线有三条,
则方程(-3x
02+12x
0-9)(x
0+1)+m=-x
03+6x
02-9x
0有三解∴m=2x
°3-3x
°2-12x
°+9,令g(x)=2x
3-3x
2-12x+9
则g′(x)=6x
2-6x-12=6(x+1)(x-2)…(12分)
易知x=-1,2为g(x)的极值大、极小值点,又g(x)
极小=-11,g(x)
极大=16,
故满足条件的m的取值范围-11<m<16.…(15分)
分析:(Ⅰ)由f′(x)=3ax
2+2bx-9,知
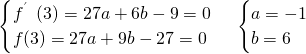
,由此能求出f
max(x).
(Ⅱ)设过P点的切线切曲线于点(x
0,y
0),则切线的斜率k=-3x
02+12x
0-9,所以切线方程为y=(-3x
02+12x
0-9)(x+1)+mw,故y
0=(-3x
02+12x
0-9)(x
0+1)+m=-x
03+6x
02-9x
0.由此能求出满足条件的m的取值范围.
点评:本题考查f(x)在区间[0,1]上的最大值和求实数m的取值范围.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

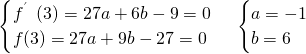
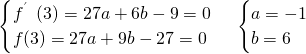 ,由此能求出fmax(x).
,由此能求出fmax(x).
