
分析 (1)若?x∈R,恒有f(x)≥λ成立,求出f(x)的最小值,即可求实数λ的取值范围;
(2)?m∈R,使得m2+2m+f(t)=0成立,f(t)≤1,再分类讨论,即可求实数t的取值范围.
解答 解:(1)f(x)=|x|+|x+1|≥1.
∵?x∈R,恒有f(x)≥λ成立,
∴λ≤1;
(2)由题意,f(t)=$\left\{\begin{array}{l}{-2t-1,t<-1}\\{1,-1≤t≤0}\\{2t+2,t>0}\end{array}\right.$,
?m∈R,使得m2+2m+f(t)=0成立,
∴△=4-4f(t)≥0,
∴f(t)≤1,
t<-1时,f(t)=-2t-1≤1,∴t≥-1,不合题意,舍去;
-1≤t≤0时,f(t)=1,此时f(t)≤1恒成立;
t>0时,f(t)=2t+1≤1,∴t≤0,不合题意,舍去;
综上所述,t的取值范围为[-1,0].
点评 本题考查绝对值不等式的解法,考查恒成立问题,考查学生分析解决问题的能力,属于中档题.


 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:选择题
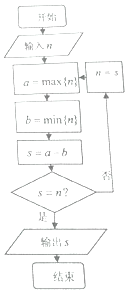 正整数的各数位上的数字重新排列后得到的最大数记为a=max{n},得到的最小数记为b=min{n}(如正整数n=2016,则a=6210,b=0126),执行如图所,示的程序框图,若输入n=2017,则输出的S的值为( )
正整数的各数位上的数字重新排列后得到的最大数记为a=max{n},得到的最小数记为b=min{n}(如正整数n=2016,则a=6210,b=0126),执行如图所,示的程序框图,若输入n=2017,则输出的S的值为( )| A. | 6174 | B. | 7083 | C. | 8341 | D. | 8352 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{7}$ | B. | 0 | C. | $\sqrt{7}$ | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
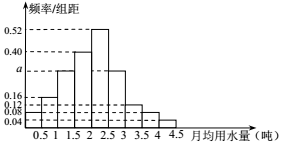 我国是世界上严重缺水的国家,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),用水量不超过 x 的部分按平价收费,超出 x 的部分按议价收费.为了了解全市居民用水量的分布情况,通过抽样,获得了 100 位居民某年的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
我国是世界上严重缺水的国家,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),用水量不超过 x 的部分按平价收费,超出 x 的部分按议价收费.为了了解全市居民用水量的分布情况,通过抽样,获得了 100 位居民某年的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com