Question

1．已知$λ=3\int_0^1{{x^2}dx}$，在矩形ABCD中，AB=2，AD=1，点P为矩形ABCD内一点，则使得$\overrightarrow{AP}•\overrightarrow{AC}≥λ$的概率为（　　）

• A． $\frac{1}{8}$
• B． $\frac{1}{4}$
• C． $\frac{3}{4}$
• D． $\frac{7}{8}$

Answer 1

分析 $λ=3\int_0^1{{x^2}dx}$=3×$\frac{1}{3}{x}^{3}{|}_{0}^{1}$=1，将矩形放在坐标系中，设P（x，y）利用向量的数量积公式，作出对应的区域，求出对应的面积即可得到结论．

解答 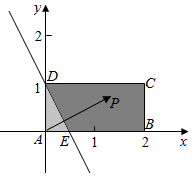解：$λ=3\int_0^1{{x^2}dx}$=3×$\frac{1}{3}{x}^{3}{|}_{0}^{1}$=1，
将矩形放在坐标系中，设P（x，y），A（0，0），C（2，1），
则$\overrightarrow{AP}•\overrightarrow{AC}≥λ$，即2x+y≥1，
作出不等式对应的区域，为五边形DCBE，
当y=0时，x=$\frac{1}{2}$，即E（$\frac{1}{2}$，0），
则△ADE的面积S=$\frac{1}{2}$×$\frac{1}{2}$×1=$\frac{1}{4}$，五边形DCBE的面积S=2-$\frac{1}{4}$=$\frac{7}{4}$
则$\overrightarrow{AP}•\overrightarrow{AC}≥λ$的概率P=$\frac{\frac{7}{4}}{2}$=$\frac{7}{8}$，
故选：D．

点评 本题主要考查几何概型的概率的计算，根据向量数量积的坐标关系，求出对应区域面积，是解决本题的关键．