
分析 (1)求出F(x)的定义域,求得导数,判断符号,即可得到所求单调区间;
(2)由题意可得该四边形为平行四边形等价于f(m)-g(m)=f(n)-g(n)且m>0,n>0.当a=-e时,$F(x)=f(x)-g(x)={e^x}+\frac{e}{x}({x>0})$,求出导数,求得单调性,确定0<m<1<n,或0<n<1<m,即可得证.
解答 解:(1)$F(x)={e^x}-\frac{a}{x}$,其定义域为(-∞,0)∪(0,+∞)
而$F'(x)={e^x}+\frac{a}{x^2}$,
当a>0时,F'(x)>0,
故F(x)的单调递增区间为(-∞,0),(0,+∞),无单调递减区间.
(2)证明:因为直线x=m与x=n平行,
故该四边形为平行四边形等价于f(m)-g(m)=f(n)-g(n)且m>0,n>0.
当a=-e时,$F(x)=f(x)-g(x)={e^x}+\frac{e}{x}({x>0})$,
则$F'(x)={e^x}-\frac{e}{x^2}$.令$g(x)=F'(x)={e^x}-\frac{e}{x^2}$,
则 $g'(x)={e^x}+\frac{2e}{x^3}>0$,
故$F'(x)={e^x}-\frac{e}{x^2}$在(0.+∞)上单调递增;
而$F'(1)=e-\frac{e}{1^2}=0$,
故x∈(0,1)时F'(x)<0,F(x)单调递减;x∈(1,+∞)时F'(x)>0,F(x)单调递增;
而F(m)=F(n),
故0<m<1<n,或0<n<1<m,
所以(m-1)(n-1)<0.
点评 本题考查导数的运用:求单调区间和单调性,考查构造函数法和转化思想的运用,考查化简整理的运算能力,属于中档题.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
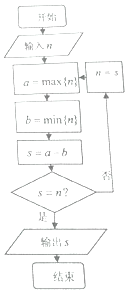 正整数的各数位上的数字重新排列后得到的最大数记为a=max{n},得到的最小数记为b=min{n}(如正整数n=2016,则a=6210,b=0126),执行如图所,示的程序框图,若输入n=2017,则输出的S的值为( )
正整数的各数位上的数字重新排列后得到的最大数记为a=max{n},得到的最小数记为b=min{n}(如正整数n=2016,则a=6210,b=0126),执行如图所,示的程序框图,若输入n=2017,则输出的S的值为( )| A. | 6174 | B. | 7083 | C. | 8341 | D. | 8352 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{2}{3}$,+∞) | B. | [$\frac{2}{3}$,1] | C. | [1,+∞) | D. | [0,1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com