
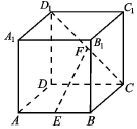
 正方体ABCD-A1B1C1D1中,E为AB中点,F为CD1中点.
正方体ABCD-A1B1C1D1中,E为AB中点,F为CD1中点.分析 (1)取DD1中点M,连接MA,MF,推导出AEFM是平行四边形,从而EF∥AM,由此能证明EF∥平面ADD1A1.
(2)三棱锥D1-DEF的体积${V_{{D_1}-DEF}}={V_{E-{D_1}DF$.由此能求出结果.
解答 证明:(1)取DD1中点M,连接MA,MF,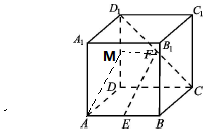
∵正方体ABCD-A1B1C1D1中,E为AB中点,F为CD1中点.
∴$MF\underline{\underline∥}AE\underline{\underline∥}\frac{1}{2}DC$,
∴AEFM是平行四边形,∴EF∥AM,
又AM?平面ADD1A1,EF?平面ADD1A1,
∴EF∥平面ADD1A1.
解:(2)∵AB=2,
∴三棱锥D1-DEF的体积:
${V_{{D_1}-DEF}}={V_{E-{D_1}DF}}=\frac{1}{3}{S_{△{D_1}DF}}×2=\frac{1}{3}×1×2=\frac{2}{3}$.
点评 本题考查线面平行的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{7}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
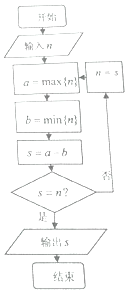 正整数的各数位上的数字重新排列后得到的最大数记为a=max{n},得到的最小数记为b=min{n}(如正整数n=2016,则a=6210,b=0126),执行如图所,示的程序框图,若输入n=2017,则输出的S的值为( )
正整数的各数位上的数字重新排列后得到的最大数记为a=max{n},得到的最小数记为b=min{n}(如正整数n=2016,则a=6210,b=0126),执行如图所,示的程序框图,若输入n=2017,则输出的S的值为( )| A. | 6174 | B. | 7083 | C. | 8341 | D. | 8352 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com