练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．求经过三点A（1，-1）、B（1，4）、C（4，2）的圆的方程．

    分析 由题意设出圆的一般式方程，把A，B，C的坐标代入圆的方程，联立方程组求得D，E，F的值得答案．

    解答 解：设过三点A（1，-1）、B（1，4）、C（4，2）的圆的方程为x2+y2+Dx+Ey+F=0，
    ∴$\left\{\begin{array}{l}{2+D-E+F=0①}\\{17+D+4E+F=0②}\\{20+4D+2E+F=0③}\end{array}\right.$，
    由①②得：E=-3 ④，
    由②③得：3D-2E+3=0 ⑤，
    把④代入⑤得：D=-3，
    把D=-3，E=-3代入①得：F=-2．
    ∴经过三点A（1，-1）、B（1，4）、C（4，2）的圆的方程为x2+y2-3x-3y-2=0．

    点评 本题考查圆的一般式方程，训练了待定系数法，是基础的计算题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

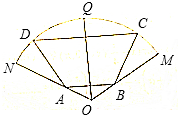    14．如图，扇形MON的半径为2，圆心角为$\frac{2}{3}$π，四边形ABCD为扇形的内接等腰梯形，其中底边AB的两个端点分别在半径ON和0M上，C、D在弧$\widehat{MQN}$上，Q为弧$\widehat{MN}$的中点，∠ABC=$\frac{2}{3}$π，求梯形ABCD面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．己知平面向量|$\overrightarrow{OA}$|=2，$\overrightarrow{OA}$与$\overrightarrow{OB}$-$\overrightarrow{OA}$的夹角为120°，$\overrightarrow{OC}$=$λ\overrightarrow{OA}$+（1-λ）$\overrightarrow{OB}$（λ∈R），求|$\overrightarrow{OC}$|的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．已知函数f（x）=x2+nx+m，若{x|f（x）=0}={x|f（f（x））=0}≠∅，则m+n的取值范围是[0，4）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．已知向量$\overrightarrow{a}$=（2，1），$\overrightarrow{a}$•$\overrightarrow{b}$=0，|$\overrightarrow{a}$+$\overrightarrow{b}$|=5$\sqrt{2}$，则|$\overrightarrow{b}$|=3$\sqrt{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知在递增等差数列{an}中，a1=2，a3是a1和a9的等比中项．
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）若bn=$\frac{1}{{（{n+1}）{a_n}}}$，Sn为数列{bn}的前n项和，是否存在实数m，使得Sn＜m对于任意的n∈N+恒成立？若存在，请求实数m的取值范围，若不存在，试说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知a，b均为正数，且a2+$\frac{1}{4}$b2=1，则a$\sqrt{1+{b}^{2}}$的最大值为$\frac{5}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．如图，四棱锥P-ABCD中，∠BAD=∠ABC=90°，BC=2AD，△PAB和△PAD都是等边三角形，则异面直线CD与PB所成角的大小为90°．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．设复数z满足（1-i）z=2i，则z在复平面内所对应的点位于第二象限．

    查看答案和解析>>

    同步练习册答案