
| A. | [$\frac{1}{4}$,$\frac{1}{2}$] | B. | ($\frac{1}{4}$,$\frac{1}{2}$) | C. | (-$\frac{1}{2}$,$\frac{1}{4}$) | D. | ($\frac{1}{4}$,$\frac{1}{2}$) |
分析 结合二次函数的性质得$\left\{\begin{array}{l}{f(-1)f(0)<0}\\{f(1)f(2)<0}\end{array}\right.$;从而解得.
解答 解:∵函数f(x)=(m-2)x2+mx+(2m+1)的两个零点分别在区间(-1,0)和区间(1,2)内,
结合二次函数的性质得,
$\left\{\begin{array}{l}{f(-1)f(0)<0}\\{f(1)f(2)<0}\end{array}\right.$;
即$\left\{\begin{array}{l}{(2m+1)(2m-1)<0}\\{(4m-1)(8m-7)<0}\end{array}\right.$,
解得:$\frac{1}{4}$<m<$\frac{1}{2}$;
故选B.
点评 本题考查了二次函数的性质应用及函数零点的判定定理的应用,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
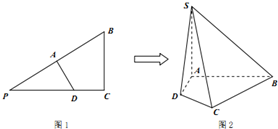 如图1,在△PBC中,∠C=90°,PC=4,BC=3,PD:DC=5:3,AD⊥PB,将△PAD沿AD边折起到SAD位置,如图2,且使SB=$\sqrt{13}$.
如图1,在△PBC中,∠C=90°,PC=4,BC=3,PD:DC=5:3,AD⊥PB,将△PAD沿AD边折起到SAD位置,如图2,且使SB=$\sqrt{13}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
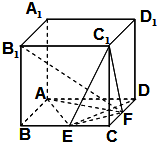 如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别是棱BC,CD的中点,
如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别是棱BC,CD的中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(a)>0 | B. | f(a)<0 | ||
| C. | f(a)可以等于0 | D. | f(a)的符号不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.5 | B. | -1.5 | C. | 2.5 | D. | -2.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com