
| A. | [0,+∞] | B. | [1,+∞] | C. | [$\frac{3}{2}$,+∞] | D. | [$\frac{1}{2}$,+∞) |
分析 根据条件可以得到M,N点的横坐标相同,且点N在直线AB上,而可以求出A,B两点的坐标,从而可以得到直线AB的方程为y=x-1,这样即可得出$|\overrightarrow{MN}|=|{x}^{2}-4x+3|$.而根据x的范围即可求出$|\overrightarrow{MN}|$的范围,即得出$|\overrightarrow{MN}|$的最大值,从而便可得出实数k的取值范围.
解答 解:由题意,M,N点的横坐标相同,$|\overrightarrow{MN}|≤k$,即$|\overrightarrow{MN}{|}_{max}≤k$;
∵A(1,0),B(3,2);
∴直线AB的方程为y=x-1;
根据题意知,点N在直线AB上;
∴$|\overrightarrow{MN}|=|{x}^{2}-3x+2-x+1|=|{x}^{2}-4x+3|$;
∵x∈[1,3],x2-4x+3=0的两根为1,3;
∴|x2-4x+3|∈[0,1];
∴$|\overrightarrow{MN}{|}_{max}=1$;
∴1≤k;
∴实数k的取值范围为[1,+∞).
故选:B.
点评 考查向量坐标的加法和数乘运算,理解“k阶线性相似”的概念,由$\overrightarrow{ON}=λ\overrightarrow{OA}+(1-λ)\overrightarrow{OB}$知N,A,B三点共线,横坐标相同的两点距离的求法,要熟悉二次函数的图象.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
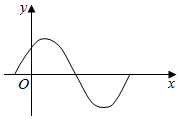
| A. | $\frac{5π}{6}$ | B. | $\frac{π}{2}$ | C. | $-\frac{π}{6}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{4}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -$\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com