
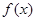 是定义在
是定义在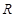 上的奇函数,当
上的奇函数,当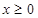 时,
时,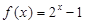 .
.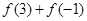 ;
;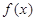 的解析式;
的解析式;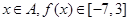 ,求区间
,求区间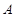 .
. 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源:不详 题型:单选题
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
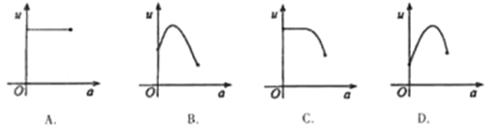
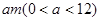 、4m,不考虑树的粗细,现在用16m长的篱笆, 借助墙角围成一个矩形的共圃ABCD,设此矩形花圃的面积为Sm2,S的最大值为
、4m,不考虑树的粗细,现在用16m长的篱笆, 借助墙角围成一个矩形的共圃ABCD,设此矩形花圃的面积为Sm2,S的最大值为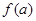 ,若将这棵树围在花圃中,则函数
,若将这棵树围在花圃中,则函数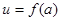 的图象大致是( )
的图象大致是( )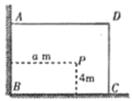
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com