练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．某企业自行设计了两条某种大型设备的生产线，分别称为1号线和2号线，经过两年的运行，每条生产线生产一台合格的该大型设备的时间数据统计如表：
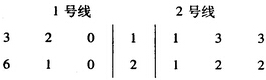
    时间（天）15～2525～3535～4545～5555～65
    1号线生产一台合格的该大型设备的频率0.10.150.450.20.1
    2号线生产一台合格的该大型设备的频率00.250.40.30.05
    其中m～n表示生产一台合格的该大型设备的时间大于m天而不超过n天，m，n为正整数．
    （1）现该企业接到甲、乙两公司各一个订单，每个公司需要生产一台合格的该大型设备，甲、乙两公司要求交货时间分别为不超过45天和55天，为了尽最大可能在甲、乙两公司订单要求的时间内交货，该企业应如何选择生产甲、乙两公司订购的该大型设备的生产线；
    （2）该企业生产的这种大型设备的质量，以其质量等级系数t来衡量，t的值越大，表明质量越好，下面是两条生产线生产的6台合格的该大型设备的质量等级系数的茎叶图．

    试从质量等级系数的平均数和方差的角度对该企业的两条生产线生产的这种合格的大型设备的质量做出分析．

    分析 （I）用Ak表示事件“k号线生产甲公司订购的合格的大型设备时，在规定的时间内交货”，用Bk表示事件“k号线生产乙公司订购的合格的大型设备时，在规定的时间内交货”，利用频率估计相应的概率可得P（A1）＞P（A2），P（B2）＞P（B1），从而得出结论；
    （II）1号与2号线生产合格的大型设备的质量等级系数的平均数都是17，再计算它们的方差，即可得出结论．

    解答 （本小题满分12分）
    解：（1）用Ak表示事件“k号线生产甲公司订购的合格的大型设备时，在规定的时间内交货”，用Bk表示事件“k号线生产乙公司订购的合格的大型设备时，在规定的时间内交货”，其中k=1，2．
    用频率估计相应的概率可得
    P（A1）=0.1+0.15+0.45=0.7，P（A2）=0.25+0.4=0.65．
    P（A1）＞P（A2），所以用1号线生产甲公司订购的合格的大型设备．
    P（B1）=1-0.1=0.9，P（B2）=0.25+0.4+0.3=0.95．
    P（B2）＞P（B1）．
    所以用2号线生产乙公司订购的合格的大型设备．（7分）
    （2）1号线与2号线生产合格的该大型设备的质量等级系数的平均数都是17．
    1号线生产合格的该大型设备的质量等级系数的方差S${\;}_{1}^{2}$=$\frac{98}{3}$，
    2号线生产合格的该大型设备的质量等级系数的方差S${\;}_{2}^{2}$=$\frac{67}{3}$，
    ∴S${\;}_{2}^{2}$＜S${\;}_{1}^{2}$．
    所以1号线与2号线生产合格的该大型设备的质量等级系数的平均数相同，但2号线生产合格的该大型设备的质量稳定性较高．（12分）

    点评 本小题主要考查极差、方差与标准差、分布的意义和作用、众数、中位数、平均数等基础知识．属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    16．圆（x-3）2+（y+1）2=1关于直线x+y-3=0对称的圆的标准方程是（x-4）2+y2=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．下列各组函数中表示同一函数的是（　　）
    A．f（x）=x-1与g（x）=$\sqrt{{{（x-1）}^2}}$B．f（x）=x与g（x）=${（\sqrt{x}）^2}$
    C．f（x）=x2-x与g（t）=t2-tD．f（x）=x-1与g（x）=$\frac{{{x^2}-1}}{x+1}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．若函数f（x）=x3+3x-1在区间[n，n+1）（n∈Z）上有零点，则n=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知焦点在y轴上的双曲线的渐近线方程是y=±4x，则该双曲线的离心率是（　　）
    A．$\sqrt{17}$B．$\sqrt{15}$C．$\frac{\sqrt{17}}{4}$D．$\frac{\sqrt{15}}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．下列命题中：
    ①若集合A={x|kx2+4x+4=0}中只有一个元素，则k=1；
    ②已知x${\;}^{\frac{1}{2}}$-x${\;}^{-\frac{1}{2}}$=2，则x2-x-2=24
    ③函数y=$\frac{1}{1-x}$在（-∞，0）上是增函数；
    ④方程2|x|=log2（x+2）+1的实根的个数是2．
    所有正确命题的序号是③④（请将所有正确命题的序号都填上）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．Sn为等差数列{an}的前n项和，a2+a8=6，则S9=（　　）
    A．108B．54C．27D．$\frac{27}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．某几何体的三视图如图所示（单位：cm），则该几何体的体积是（　　）
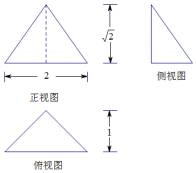
    A．$\frac{\sqrt{2}}{3}$cm3B．$\frac{2\sqrt{2}}{3}$cm3C．$\sqrt{2}c{m^3}$D．$2\sqrt{2}c{m^3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知点A，B分别是双曲线$C：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的左、右顶点，点P是双曲线C上异于A，B的另外一点，且△ABP是顶角为120°的等腰三角形，则该双曲线的渐近线方程为（　　）
    A．$\sqrt{3}$x±y=0B．x±$\sqrt{3}$y=0C．x±y=0D．$\sqrt{2}$x±y=0

    查看答案和解析>>

    同步练习册答案