
 的底面
的底面 是矩形,
是矩形, ⊥平面
⊥平面 ,
, ,
,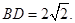

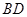 ⊥平面
⊥平面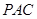 ;
;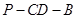 的大小;
的大小; 到平面
到平面 的距离.
的距离.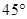 ;(3)
;(3)
 中,
中, ,
,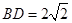 ,
,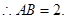
 为正方形,因此
为正方形,因此 . ∵
. ∵ ⊥平面
⊥平面 ,
, 平面
平面 ,
,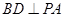 .又∵
.又∵ , ∴
, ∴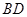 ⊥平面
⊥平面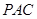 . ……4分
. ……4分  ⊥平面
⊥平面 ,知
,知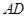 为
为 在平面
在平面 内的射影,
内的射影, ,∴
,∴ ,知
,知 为二面角
为二面角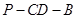 的平面角.
的平面角.  ,∴
,∴ . ……9分
. ……9分  ,∴
,∴ ,
, 到面
到面 的距离为
的距离为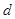 ,
, ,有
,有 ,
, 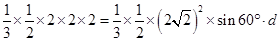 ,
, . ……14分
. ……14分 
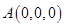 、
、 、
、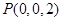 .
. 中,
中, ,
,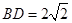 ,
,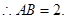 ∴
∴ ,
,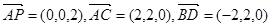 ∵
∵ ,
, ,又∵
,又∵ , ∴
, ∴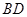 ⊥平面
⊥平面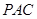 . ……4分
. ……4分 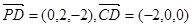 .
.  的法向量为
的法向量为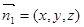 ,则
,则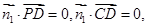
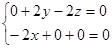 ,∴
,∴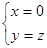 故平面
故平面 的法向量可取为
的法向量可取为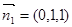
 ⊥平面
⊥平面 ,∴
,∴ 为平面
为平面 的法向量.
的法向量. 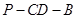 的大小为
的大小为 ,依题意可得
,依题意可得 ,
, ……9分
……9分 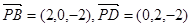 ,
, 的法向量为
的法向量为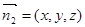 ,
, ,即
,即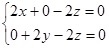 ,∴
,∴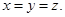 ,
, 的法向量可取为
的法向量可取为 .
.  ,∴
,∴ 到面
到面 的距离为
的距离为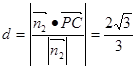 . ……14分
. ……14分

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源:不详 题型:解答题
 ,O为AB的中点.
,O为AB的中点.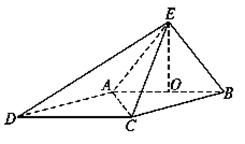
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
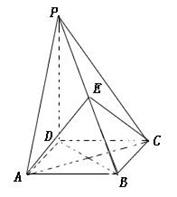
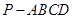 的底面是正方形,
的底面是正方形,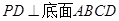 ,点E在棱PB上.若AB=
,点E在棱PB上.若AB=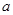 ,
,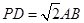
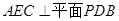 ;
; 
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
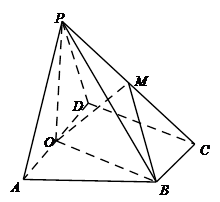
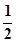 AD=1,CD=
AD=1,CD=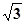 .
.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
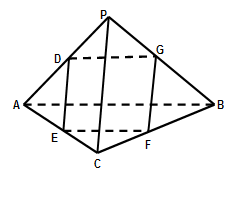
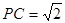 ,求四面体PABC的体积.
,求四面体PABC的体积.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
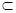 M,b
M,b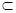 M,且c⊥a,c⊥b,则c⊥M ④若a⊥M, a//N,则M⊥N,其中正确命题的个数为( )
M,且c⊥a,c⊥b,则c⊥M ④若a⊥M, a//N,则M⊥N,其中正确命题的个数为( )| A.0个 | B.1个 | C.2个 | D.3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com