
分析 (1)利用线段垂直平分线的性质推出|NC+|NA|=|NC|+|NM|=2$\sqrt{2}$>2=|CA|,再利用椭圆的定义知,点N的轨迹是以A、C 为焦点的椭圆,利用待定系数法求出椭圆的方程
(2)不妨设FH斜率为k,且将原点移至F,则直线FH方程为y=kx,则椭圆方程变为$\frac{{x}^{2}}{2}$+(y-2)2=1,将直线与椭圆方程联立得(1+2k2)x2-8kx+6=0,结合题设条件求参数λ的范围.
解答 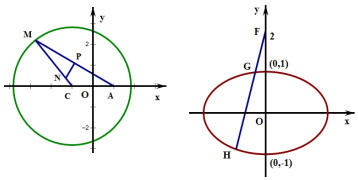 解:(1)因为|AP|=|PM|,NP⊥MA,
解:(1)因为|AP|=|PM|,NP⊥MA,
所以NP为线段AM的垂直平分线,|NA|=|NM|,|NC+|NA|=|NC|+|NM|=2$\sqrt{2}$>2=|CA|,
所以动点N的轨迹是以C(-1,0),A(1,0)为焦点的椭圆,…..(3分)
且长轴长为2A=2$\sqrt{2}$,焦距2c=2,所以A=$\sqrt{2}$,c=1,b2=1,
曲线E的方程为$\frac{{x}^{2}}{2}+{y}^{2}$=1…(5分)
(2)当斜率不存在时,直线与曲线E有2个交点此时参数的值为$λ=\frac{1}{3}$,
不妨设FH斜率为k,且将原点移至F,
则直线FH方程为y=kx,椭圆方程变为$\frac{{x}^{2}}{2}$+(y-2)2=1,
将直线方程代入椭圆得$\frac{{x}^{2}}{2}$+(kx-2)2=1,整理得(1+2k2)x2-8kx+6=0,
直线与曲线E有二不同的交点,故△=(-8k)2-4•6(1+2k2)=16k2-24>0,即k2>$\frac{3}{2}$,
因为左右对称,可以研究单侧,
当k>0时,λ=$\frac{{x}_{1}}{{x}_{2}}$=$\frac{-8k-\sqrt{16{k}^{2}-24}}{8k+\sqrt{16{k}^{2}-24}}$=$\frac{2-\sqrt{1-\frac{3}{2{k}^{2}}}}{2+\sqrt{1-\frac{3}{2{k}^{2}}}}$,
令t=$\sqrt{1-\frac{3}{2{k}^{2}}}$∈(0,1),则λ=$\frac{2-t}{2+t}$,t∈(0,1),
由于λ=$\frac{4}{2+t}$-1,故函数在t∈(0,1)上是减函数,故$\frac{1}{3}<λ<1$,
综上,实数λ的取值范围是$\frac{1}{3}≤λ<1$.
点评 本题考查椭圆的定义的应用,轨迹方程的求法,考查计算能力.解题的关键是掌握圆锥曲线的定义,由题设条件判断出所求的轨迹是椭圆,以及能将求两线段比值的问题转化为坐标比值,以利于用直线与圆锥曲线的方程研究参数的取值范围


科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 1 | C. | -3或1 | D. | 3或1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
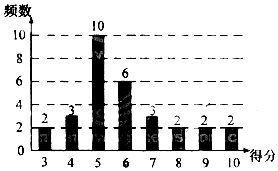 为了普及环保知识,增强环保意识,某大学随即抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为m,众数为n,平均值为$\overline{x}$,则( )
为了普及环保知识,增强环保意识,某大学随即抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为m,众数为n,平均值为$\overline{x}$,则( )| A. | m=n=$\overline{x}$ | B. | m=n<$\overline{x}$ | C. | m<n<$\overline{x}$ | D. | n<m<$\overline{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{12}{5}$ | B. | 4 | C. | $-\frac{12}{5}$ | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若α,β垂直于同一平面,则α与β平行 | |
| B. | 若m,n平行于同一平面,则m与n平行 | |
| C. | 若m,n不平行,则m与n不可能垂直于同一平面 | |
| D. | 若α,β不平行,则在α内不存在与β平行的直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{7}$(8n-1) | B. | $\frac{2}{7}$(8n+1-1) | C. | $\frac{2}{7}$(8n+3-1) | D. | $\frac{2}{7}$(8n+4-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com