
| A�� | $\frac{12}{5}$ | B�� | 4 | C�� | $-\frac{12}{5}$ | D�� | -4 |
���� ��������$\overrightarrow{a}$������$\overrightarrow{b}$�ϵ�ͶӰ���壬���㼴�ɣ�
��� �⣺��|$\overrightarrow{a}$|=3��|$\overrightarrow{b}$|=5����$\overrightarrow{a}•\overrightarrow{b}$=12��
������$\overrightarrow{a}$������$\overrightarrow{b}$�ϵ�ͶӰΪ
|$\overrightarrow{a}$|cos��$\overrightarrow{a}$��$\overrightarrow{b}$��=|$\overrightarrow{a}$|��$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|��|\overrightarrow{b}|}$
=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}$
=$\frac{12}{5}$��
��ѡ��A��
���� ���⿼������һ��������һ�����ϵ�ͶӰ���⣬����ʱӦ����ͶӰ��ʽ���м��㣬�ǻ����⣮


 �¿α�����Ķ�ѵ��ϵ�д�
�¿α�����Ķ�ѵ��ϵ�д� ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3�� | B�� | $\frac{3��}{2}$ | C�� | 6�� | D�� | $\frac{3��}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
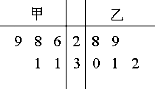 Ϊ�Ƚϼס�������ij��14ʱ������״�������ѡȡ�����е�5�죬����5����14ʱ���������ݣ���λ���棩�Ƴ���ͼ��ʾ�ľ�Ҷͼ���������½��ۣ�
Ϊ�Ƚϼס�������ij��14ʱ������״�������ѡȡ�����е�5�죬����5����14ʱ���������ݣ���λ���棩�Ƴ���ͼ��ʾ�ľ�Ҷͼ���������½��ۣ�| A�� | �٢� | B�� | �٢� | C�� | �ڢ� | D�� | �ڢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
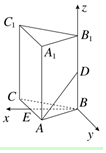 ����������ABC-A1B1C1�У���֪AB=1��D����BB1�ϣ���BD=1����AD��ƽ��AA1C1C���ɵĽǵ�����ֵΪ$\frac{\sqrt{6}}{4}$��
����������ABC-A1B1C1�У���֪AB=1��D����BB1�ϣ���BD=1����AD��ƽ��AA1C1C���ɵĽǵ�����ֵΪ$\frac{\sqrt{6}}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��1] | B�� | ��0��2�� | C�� | $��{0��\frac{3}{2}}]$ | D�� | ��0��2] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��2�� | B�� | ��2��1�� | C�� | ��-1��2�� | D�� | ��-2��-1�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com