
分析 ①利用命题的否定定义即可判断出结论.
②若2a<2b,则a<b,当a或b为负数时,log${\;}_{\frac{1}{2}}$a>log${\;}_{\frac{1}{2}}$b不成立,若log${\;}_{\frac{1}{2}}$a>log${\;}_{\frac{1}{2}}$b,利用对数函数的单调性即可得出a,b的大小关系.
③利用三角函数的平移变换即可判断出正误.
④由题可知,$\overrightarrow{a}•\overrightarrow{b}$=-1,再利用$|\overrightarrow{a}+\overrightarrow{b}{|}^{2}$=${\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}$+${\overrightarrow{b}}^{2}$即可得出.
解答 解:①利用命题的否定定义可知:正确.
②若2a<2b,则a<b,当a或b为负数时,log${\;}_{\frac{1}{2}}$a>log${\;}_{\frac{1}{2}}$b不成立,若log${\;}_{\frac{1}{2}}$a>log${\;}_{\frac{1}{2}}$b,∴0<a<b,∴2a<2b.故②正确.
③把y=sin(-3x)的图象上所有点向右平移$\frac{π}{4}$,得到y=sin$sin[-(x-\frac{π}{4})]$=$sin(-3x+\frac{3π}{4})$,故③不正确.
④由题可知,$\overrightarrow{a}•\overrightarrow{b}$=1×2 cos$\frac{2π}{3}$=-1,∴$|\overrightarrow{a}+\overrightarrow{b}{|}^{2}$=${\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}$+${\overrightarrow{b}}^{2}$=3,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{3}$,故④正确.
故答案为:①②④.
点评 本题考查了简易逻辑的判定方法、函数的单调性、三角函数平移变换、向量数量积运算性质,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 第x天 | 1 | 2 | 3 | 4 | 5 |
| 被感染的计算机数量y(台) | 12 | 24 | 49 | 95 | 190 |
| A. | y=12x | B. | y=6x2-6x+12 | C. | y=6•2x | D. | y=12log2x+12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
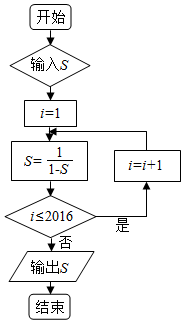
| A. | -1 | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com