
分析 设向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为θ,根据向量的数量积公式计算即可.
解答 解:∵$|{2\overrightarrow a-\overrightarrow b}|=\sqrt{2}$,
∴${({2\overrightarrow a-\overrightarrow b})^2}=2$,
∵$\overrightarrow a,\overrightarrow b$为单位向量,即${\overrightarrow{4a}^2}-4\overrightarrow a•\overrightarrow b+{\overrightarrow b^2}=2$,
∴4-4cosθ+1=2,
∴$cosθ=\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 本题考查向量的夹角的计算,考查向量数量积公式的运用,属于基础题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
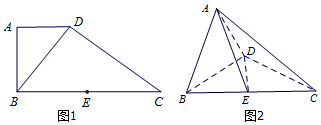 如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体.
如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 身高x(cm) | 60 | 70 | 80 | 90 | 100 | 110 |
| 体重y(kg) | 6 | 8 | 10 | 14 | 15 | 18 |
| ${\widehate^{(1)}}$ | 0.41 | 0.01 | 1.21 | -0.19 | 0.41 | |
| ${\widehate^{(2)}}$ | -0.36 | 0.07 | 0.12 | 1.69 | -0.34 | -1.12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com