
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 切线斜率中的最大值;
切线斜率中的最大值;
(Ⅱ)若关于![]() 的方程
的方程![]() 有解,求实数
有解,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】(数学文卷·2017届湖北省黄冈市高三上学期期末考试第16题) “中国剩余定理”又称“孙子定理”.1852年英国来华传教伟烈亚利将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法符合1801年由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”. “中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将2至2017这2016个数中能被3除余1且被5除余1的数按由小到大的顺序排成一列,构成数列![]() ,则此数列的项数为__________.
,则此数列的项数为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一个三角形的平行投影仍是三角形,则下列命题:
①三角形的高线的平行投影,一定是这个三角形的平行投影的高线;
②三角形的中线的平行投影,一定是这个三角形的平行投影的中线;
③三角形的角平分线的平行投影,一定是这个三角形的平行投影的角平分线;
④三角形的中位线的平行投影,一定是这个三角形的平行投影的中位线.
其中正确的命题有 ( )
A. ①② B. ②③
C. ③④ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P—ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知BD=2AD=8,AB=2DC=4![]() .
.
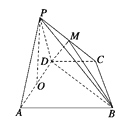
(1)设M是PC上的一点,求证:平面MBD⊥平面PAD;
(2)求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费的方法计算:电费每月用电不超过100度时,按每度0.57元计算;每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.5元计算.
(Ⅰ)设月用电![]() 度时,应交电费
度时,应交电费![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(Ⅱ)小明家第一季度缴纳电费情况如下:
月份 | 一月 | 二月 | 三月 | 合计 |
交费金额 | 76元 | 63元 | 45.6元 | 184.6元 |
问小明家第一季度共用电多少度?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在高一年级学生中,对自然科学类、社会科学类校本选修课程的选课意向进行调查.现从高一年级学生中随机抽取![]() 名学生,其中男生
名学生,其中男生![]() 名;在这名
名;在这名![]() 学生中选择社会科学类的男生、女生均为
学生中选择社会科学类的男生、女生均为![]() 名.
名.
(1)试问:从高一年级学生中随机抽取![]() 人,抽到男生的概率约为多少?
人,抽到男生的概率约为多少?
(2)根据抽取的![]() 名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过
名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过![]() 的前提下认为科类的选择与性别有关?
的前提下认为科类的选择与性别有关?
选择自然科学类 | 选择社会科学类 | 合计 | |
男生 | |||
女生 | |||
合计 |
附: 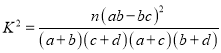 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,内角
中,内角![]() 的对边分别是
的对边分别是![]() ,已知
,已知![]() 为锐角,且
为锐角,且![]() .
.
(Ⅰ)求![]() 的大小;
的大小;
(Ⅱ)设函数![]() ,其图象上相邻两条对称轴间的距离为
,其图象上相邻两条对称轴间的距离为![]() .将函数
.将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,求函数
的图象,求函数![]() 在区间
在区间![]() 上的值域.
上的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com