解:(I)依题意,f(x)=g(x),即ax
2+ax=x-a,
整理,得ax
2+(a-1)x+a=0,①
∵a≠0,函数f(x)与g(x)图象相交于不同的两点A、B,
∴△>0,即△=(a-1)
2-4a
2=-3a
2-2a+1=(3a-1)(-a-1)>0.
∴-1<a<

且a≠0.
设A(x
1,y
1),B(x
2,y
2),且x
1<x
2,由①得,x
1•x
2=1>0,x
1+x
2=-

.
设点O到直线g(x)=x-a的距离为d,则d=
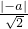
,
∴S
△OAB=
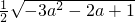
=
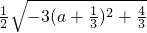
.
∵∴-1<a<

且a≠0,∴当a=-

时,S
△OAB有最大值

;
(II)证明:由题意可知f(x)-g(x)=a(x-p)(x-q)
∴f(x)-(p-a)=a(x-p)(x-q)+x-a-(p-a)=(x-p)(ax-aq+1),
当x∈(0,p)时,x-p<0,且ax-aq+1>1-aq>0,
∴f(x)-(p-a)<0,
∴f(x)<p-a.
分析:(I)依题意,f(x)=g(x),函数f(x)与g(x)图象相交于不同的两点A、B,则△>0,求出a的范围,设A(x
1,y
1),B(x
2,y
2),求出AB以及点O到直线g(x)=x-a的距离,从而求出三角形的面积关于a的函数,根据a的范围求出面积的最值;
(II)由f(x)-g(x)=a(x-p)(x-q),以及g(x)=x-a,表示出f(x),代入f(x)-(p-a)中,因式分解后,判定其积小于0,从而得到f(x)小于p-a,得证.
点评:本题考查了三角形面积的计算,以及利用二次函数研究函数的最值,考查不等式的证明.根据题意设出f(x)-g(x)是解本题的关键,证明不等式的方法是灵活运用“作差法”,属于中档题.

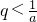 ,证明:当x∈(0,P)时,f(x)<P-a.
,证明:当x∈(0,P)时,f(x)<P-a. 且a≠0.
且a≠0. .
.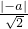 ,
,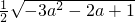 =
=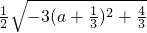 .
. 且a≠0,∴当a=-
且a≠0,∴当a=- 时,S△OAB有最大值
时,S△OAB有最大值 ;
;

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案