
【题目】已知函数![]() ,在区间
,在区间![]() 内任取两个实数
内任取两个实数![]() ,
,![]() ,且
,且![]() ,若不等式
,若不等式![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是
的取值范围是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
分析:首先,由![]() 的几何意义,得到直线的斜率,然后,得到函数图象上在区间(1,2)内任意两点连线的斜率大于1,从而得到f′(x)=
的几何意义,得到直线的斜率,然后,得到函数图象上在区间(1,2)内任意两点连线的斜率大于1,从而得到f′(x)=![]() >1 在(1,2)内恒成立.分离参数后,转化成 a>2x2+3x+1在(1,2)内恒成立.从而求解得到a的取值范围.
>1 在(1,2)内恒成立.分离参数后,转化成 a>2x2+3x+1在(1,2)内恒成立.从而求解得到a的取值范围.
详解:∵![]() 的几何意义为:
的几何意义为:
表示点(p+1,f(p+1)) 与点(q+1,f(q+1))连线的斜率,
∵实数p,q在区间(0,1)内,故p+1 和q+1在区间(1,2)内.
不等式![]() >1恒成立,
>1恒成立,
∴函数图象上在区间(1,2)内任意两点连线的斜率大于1,
故函数的导数大于1在(1,2)内恒成立.
由函数的定义域知,x>﹣1,
∴f′(x)=![]() >1 在(1,2)内恒成立.
>1 在(1,2)内恒成立.
即 a>2x2+3x+1在(1,2)内恒成立.
由于二次函数y=2x2+3x+1在[1,2]上是单调增函数,
故 x=2时,y=2x2+3x+1在[1,2]上取最大值为15,
∴a≥15
∴a∈[15,+∞).
故选:A.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() ,圆
,圆![]() .
.
(1)若过点![]() 的直线
的直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设动圆![]() 同时平分圆
同时平分圆![]() 的周长、圆
的周长、圆![]() 的周长.
的周长.
①证明:动圆圆心![]() 在一条定直线上运动;
在一条定直线上运动;
②动圆![]() 是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设某士兵远程射击一个易爆目标,射击一次击中目标的概率为![]() ,三次射中目标或连续两次射中目标,该目标爆炸,停止射击,否则就一直独立地射击至子弹用完.现有5发子弹,设耗用子弹数为随机变量X.
,三次射中目标或连续两次射中目标,该目标爆炸,停止射击,否则就一直独立地射击至子弹用完.现有5发子弹,设耗用子弹数为随机变量X.
(1)若该士兵射击两次,求至少射中一次目标的概率;
(2)求随机变量X的概率分布与数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知表1是某年部分日期的天安门广场升旗时刻表.
表1:某年部分日期的天安门广场升旗时刻表

将表1中的升旗时刻化为分数后作为样本数据(如:![]() 可化为
可化为![]() ).
).
(Ⅰ)请补充完成下面的频率分布表及频率分布直方图;
|
|
(Ⅱ)若甲学校从上表日期中随机选择一天观看升旗.试估计甲学校观看升旗的时刻早于6:00的概率;
(Ⅲ)若甲,乙两个学校各自从表1中五月、六月的日期中随机选择一天观看升旗, 求两校观看升旗的时刻均不早于5:00的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面几何中,通常将完全覆盖某平面图形且直径最小的圆,称为该平面图形的最小覆盖圆.最小覆盖圆满足以下性质:①线段![]() 的最小覆盖圆就是以
的最小覆盖圆就是以![]() 为直径的圆;②锐角
为直径的圆;②锐角![]() 的最小覆盖圆就是其外接圆.已知曲线
的最小覆盖圆就是其外接圆.已知曲线![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为曲线
为曲线![]() 上不同的四点.
上不同的四点.
(Ⅰ)求实数![]() 的值及
的值及![]() 的最小覆盖圆的方程;
的最小覆盖圆的方程;
(Ⅱ)求四边形![]() 的最小覆盖圆的方程;
的最小覆盖圆的方程;
(Ⅲ)求曲线![]() 的最小覆盖圆的方程.
的最小覆盖圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知边长为![]() 的正
的正![]() 的顶点
的顶点![]() 在平面
在平面![]() 内,顶点
内,顶点![]() ,
,![]() 在平面
在平面![]() 外的同一侧,点
外的同一侧,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 在平面
在平面![]() 内的投影,设
内的投影,设![]() ,直线
,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .若
.若![]() 是以角
是以角![]() 为直角的直角三角形,则
为直角的直角三角形,则![]() 的最小值为__________.
的最小值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长方形ABCD如图1中,AD= ![]() ,AB=2,E为AB中点,将△ADE沿DE折起到△PDE,所得四棱锥P﹣BCDE如图2所示.
,AB=2,E为AB中点,将△ADE沿DE折起到△PDE,所得四棱锥P﹣BCDE如图2所示.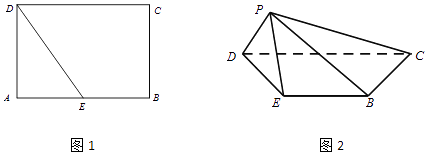
(Ⅰ)若点M为PC中点,求证:BM∥平面PDE;
(Ⅱ)当平面PDE⊥平面BCDE时,求三棱锥E﹣PCD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com