
【题目】已知![]() ,
, ![]() .
.
(1)当n=1,2,3时,分别比较f(n)与g(n)的大小(直接给出结论);
(2)由(1)猜想f(n)与g(n)的大小关系,并证明你的结论.
【答案】(1)当n=1时,f(1)>g(1);当n=2时,f(2)>g(2);当n=3时,f(3)>g(3);
(2)猜想: ![]() ,证明见结论.
,证明见结论.
【解析】(1)当n=1时,f(1)>g(1);当n=2时,f(2)>g(2);当n=3时,f(3)>g(3).
(2)猜想:f(n)>g(n)(n∈N*),即1+![]() >2(
>2(![]() -1)(n∈N*).
-1)(n∈N*).
下面用数学归纳法证明:①当n=1时,f(1)=1,g(1)=2(![]() -1),f(1)>g(1).
-1),f(1)>g(1).
②假设当n=k时,猜想成立,即1+![]() >2(
>2(![]() -1).
-1).
则当n=k+1时,f(k+1)=1+![]() +
+![]() >2(
>2(![]() -1)+
-1)+![]() =2
=2![]() +
+![]() -2,而g(k+1)=2(
-2,而g(k+1)=2(![]() -1)=2
-1)=2![]() -2,
-2,
下面转化为证明: ![]() .
.
只要证:2(k+1)+1=2k+3>2![]() ,
,
需证:(2k+3)2>4(k+2)(k+1),即证:4k2+12k+9>4k2+12k+8,此式显然成立.
所以,当n=k+1时猜想也成立.综上可知:对n∈N*,猜想都成立,
即1+![]() (n∈N*)成立.
(n∈N*)成立.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:高中数学 来源: 题型:
【题目】潮州统计局就某地居民的月收入调查了![]() 人,并根据所得数据画了样本的频率分
人,并根据所得数据画了样本的频率分
布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在![]() )。
)。

(1)求居民月收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这![]() 人中分层抽样方法抽出
人中分层抽样方法抽出![]() 人作进一步分析,则月收入在
人作进一步分析,则月收入在![]() 的这段应抽多少人?
的这段应抽多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题错误的是( )
A. 如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 内所有直线都垂直于平面
内所有直线都垂直于平面![]()
B. 如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 内一定存在直线平行于平面
内一定存在直线平行于平面![]()
C. 如果平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,那么
,那么![]() 平面
平面![]()
D. 如果平面![]() 不垂直于平面
不垂直于平面![]() ,那么平面
,那么平面![]() 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在(0,2π)内,使sinx﹣cosx<0成立的x取值范围是( )
A.( ![]() ,
, ![]() )
)
B.(0, ![]() )
)
C.( ![]() ,π)∪(
,π)∪( ![]() ,2π)
,2π)
D.(0, ![]() )∪(
)∪( ![]() ,2π)
,2π)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π,x∈R)在一个周期内的图象如图所示,则函数的解析式为 . 直线y= ![]() 与函数y=f(x)(x∈R)图象的所有交点的坐标为 .
与函数y=f(x)(x∈R)图象的所有交点的坐标为 . 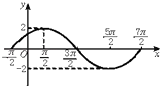
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱(侧棱与底面垂直的棱柱)ABC﹣A1B1C1中,点G是AC的中点.

(1)求证:B1C∥平面 A1BG;
(2)若AB=BC, ![]() ,求证:AC1⊥A1B.
,求证:AC1⊥A1B.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=sin(2ωx+φ)(ω>0,0<φ<π)的最小正周期为π,且函数图象关于点(﹣ ![]() ,0)对称,则函数的解析式为( )
,0)对称,则函数的解析式为( )
A.y=sin(4x+ ![]() )
)
B.y=sin(2x+ ![]() )
)
C.y=sin(2x+ ![]() )
)
D.y=sin(4x+ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,已知在菱形![]() 中,
中, ![]() ,
, ![]() 为
为![]() 的中点,现将四边形
的中点,现将四边形![]() 沿
沿![]() 折起至
折起至![]() ,如图2.
,如图2.

(1)求证: ![]() 面
面![]() ;
;
(2)若二面角![]() 的大小为
的大小为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图. 为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”.
(1)求在这10个卖场中,甲型号电视机的“星级卖场”的个数;
(2)若在这10个卖场中,乙型号电视机销售量的平均数为26.7,求a>b的概率;
(3)若a=1,记乙型号电视机销售量的方差为![]() ,根据茎叶图推断b为何值时,
,根据茎叶图推断b为何值时,![]() 达到最值.
达到最值.
(只需写出结论)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com