
【题目】如图,直三棱柱(侧棱与底面垂直的棱柱)ABC﹣A1B1C1中,点G是AC的中点.

(1)求证:B1C∥平面 A1BG;
(2)若AB=BC, ![]() ,求证:AC1⊥A1B.
,求证:AC1⊥A1B.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)连结![]() ,交
,交![]() 于点
于点![]() ,连结
,连结![]() ,由三角形中位线定理得
,由三角形中位线定理得![]() ,由此能证明
,由此能证明![]() 平面
平面![]() ;(2)由线面垂直得
;(2)由线面垂直得![]() ,由已知推导出
,由已知推导出![]() ,从而得到
,从而得到![]() ,由此能证明
,由此能证明![]() .
.
试题解析:(1)证明:连结AB1,交A1B于点O,连结OG,在△B1AC中,∵G、O分别为AC、AB1中点,∴OG∥B1C,又∵OG平面A1BG,B1C平面A1BG,∴B1C∥平面 A1BG.
(2)证明:∵直三棱柱ABC﹣A1B1C1中,AA1⊥底面ABC,BG平面ABC,∴AA1⊥BG,∵G为棱AC的中点,AB=BC,∴BG⊥AC,∵AA1∩AC=A,∴BG⊥平面ACC1A1,∴BG⊥AC1,∵G为棱AC中点,设AC=2,则AG=1,∵![]() ,∴在Rt△ACC1和Rt△A1AG中,
,∴在Rt△ACC1和Rt△A1AG中,![]() ,∴∠AC1C=∠A1GA=∠A1GA+∠C1AC=90°,∴A1G⊥AC1,∵
,∴∠AC1C=∠A1GA=∠A1GA+∠C1AC=90°,∴A1G⊥AC1,∵![]() ,∴AC1⊥平面A1BG,∵A1B平面A1BG,∴AC1⊥A1B.
,∴AC1⊥平面A1BG,∵A1B平面A1BG,∴AC1⊥A1B.


科目:高中数学 来源: 题型:
【题目】下表是某校高三一次月考5个班级的数学、物理的平均成绩:
班级 | 1 | 2 | 3 | 4 | 5 |
数学( | 111 | 113 | 119 | 125 | 127 |
物理( | 92 | 93 | 96 | 99 | 100 |
(Ⅰ)一般来说,学生的物理成绩与数学成绩具有线性相关关系,根据上表提供的数据,求两个变量![]() ,
, ![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)从以上5个班级中任选两个参加某项活动,设选出的两个班级中数学平均分在115分以上的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:  ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
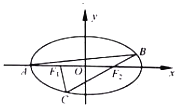
【题目】如图,设点![]() ,
, ![]() ,
, ![]() 分别为椭圆
分别为椭圆![]() 的左顶点和左,右焦点,过点
的左顶点和左,右焦点,过点![]() 作斜率为
作斜率为![]() 的直线交椭圆于另一点
的直线交椭圆于另一点![]() ,连接
,连接![]() 并延长交椭圆于点
并延长交椭圆于点![]() .
.
(1)求点![]() 的坐标(用
的坐标(用![]() 表示);
表示);
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() .
.
(1)当n=1,2,3时,分别比较f(n)与g(n)的大小(直接给出结论);
(2)由(1)猜想f(n)与g(n)的大小关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某校组织的“共筑中国梦”竞赛活动中,甲、乙两班各有6名选手参赛,在第一轮笔试环节中,评委将他们的笔试成绩作为样本数据,绘制成如图所示的茎叶图,为了增加结果的神秘感,主持人故意没有给出甲、乙两班最后一位选手的成绩,只是告诉大家,如果某位选手的成绩高于90分(不含90分),则直接“晋级”.
(1)求乙班总分超过甲班的概率;
(2)主持人最后宣布:甲班第六位选手的得分是90分,乙班第六位选手的得分是97分.若主持人从甲乙两班所有选手成绩中分别随机抽取2个,记抽取到“晋级”选手的总人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() ).
).
(1)若函数![]() 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数![]() 的取值范围;
的取值范围;
(2)求函数![]() 的极值点;
的极值点;
(3)令![]() ,
, ![]() ,设
,设![]() ,
, ![]() ,
, ![]() 是曲线
是曲线![]() 上相异三点,其中
上相异三点,其中![]() .求证:
.求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A、B、C所对的边分别为a、b、c,已知a=1,b=2, cosC=![]() .
.
(I) 求△ABC的周长; (II)求cos(A﹣C)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com