
【题目】已知函数 ![]() .
.
(Ⅰ)当 ![]() 时,求函数
时,求函数 ![]() 在
在 ![]() 处的切线方程;
处的切线方程;
(Ⅱ)试判断函数 ![]() 零点的个数.
零点的个数.
【答案】解:(Ⅰ)当 ![]() 时,
时, ![]() ,
, ![]() ,
,
∵ ![]() ,
, ![]() ,∴
,∴ ![]() 在
在 ![]() 处的切线方程为
处的切线方程为 ![]() ,即
,即 ![]() ;
;
(Ⅱ)由题知, ![]() 的定义域为
的定义域为 ![]() ,
,![]() .
.
①当 ![]() 时,对于定义域中任意
时,对于定义域中任意 ![]() ,有
,有 ![]() ,
, ![]() 在
在 ![]() 上是增函数.
上是增函数.
又 ![]() ,并且当
,并且当 ![]() 时,
时, ![]() ,∴
,∴ ![]() 有唯一的零点;
有唯一的零点;
②当 ![]() 时,在
时,在 ![]() 上
上 ![]() ,
, ![]() 单调递减;在
单调递减;在 ![]() 上,
上, ![]() ,
, ![]() 单调递增.
单调递增.
又当 ![]() 时,
时, ![]() ,并且
,并且 ![]() .这是因为:
.这是因为:![]()
![]() .
.
设 ![]() ,则
,则 ![]() .记
.记 ![]() ,则
,则 ![]() .
.
∵在 ![]() 上,
上, ![]() ,
, ![]() 单调递减;在
单调递减;在 ![]() 上,
上, ![]() ,
, ![]() 单调递增,
单调递增,
∴ ![]() 的最小值为
的最小值为 ![]() ,即
,即 ![]() 成立,∴在区间
成立,∴在区间 ![]() 内存在一点
内存在一点 ![]() ,使得
,使得 ![]() .
.
则函数 ![]() 零点的个数取决于
零点的个数取决于 ![]() 的最小值的正负.又函数
的最小值的正负.又函数 ![]() 的最小值为
的最小值为 ![]() .记
.记 ![]() ,则
,则 ![]() 是
是 ![]() 上的增函数.又观察,得
上的增函数.又观察,得 ![]() ,∴当
,∴当 ![]() 时,
时, ![]() 的最小值小于0,即
的最小值小于0,即 ![]() 有两个零点;
有两个零点;
当 ![]() 时,
时, ![]() 的最小值为0,
的最小值为0, ![]() 有唯一的零点;当
有唯一的零点;当 ![]() 时,
时, ![]() 的最小值大于0,
的最小值大于0, ![]() 没有零点.
没有零点.
综上所述,当 ![]() 或
或 ![]() 时,
时, ![]() 有唯一的零点;当
有唯一的零点;当 ![]() 时,
时, ![]() 有两个零点;当
有两个零点;当 ![]() 时,
时, ![]() 没有零点
没有零点
【解析】(1)由题意把a的值代入函数的解析式,对其求导并把x=1的值代入导函数的代数式,求出切线的方程的斜率再由点斜式求出直线的方程。(2)首先求出原函数的导函数,对a分情况讨论出导函数的正负进而得出原函数的单调性,从而得出原函数的零点存在情况即可。


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)(x∈R)满足f(1)=1,且f(x)的导函数f′(x)< ![]() ,则f(x)<
,则f(x)< ![]() 的解集为( )
的解集为( )
A.{x|-1<x<1}
B.{x|x<-1}
C.{x|x<-1,或x>1}
D.{x|x>1}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校高中男生中随机选取100名学生,将他们的体重(单位: ![]() )数据绘制成频率分布直方图,如图所示.
)数据绘制成频率分布直方图,如图所示.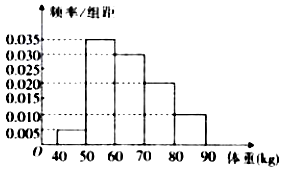
(1)估计该校的100名同学的平均体重(同一组数据以该组区间的中点值作代表);
(2)若要从体重在 ![]() ,
, ![]() ,
, ![]() 三组内的男生中,用分层抽样的方法选取6人组成一个活动队,再从这6人中选2人当正副队长,求这2人中至少有1人体重在
三组内的男生中,用分层抽样的方法选取6人组成一个活动队,再从这6人中选2人当正副队长,求这2人中至少有1人体重在 ![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市某小学三年级有甲、乙两个班,其中甲班有男生30人,女生20人,乙班有男生25人,女生25人,现在需要各班按男、女生分层抽取 ![]() 的学生进行某项调查,则两个班共抽取男生人数是 .
的学生进行某项调查,则两个班共抽取男生人数是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
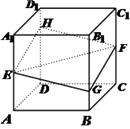
【题目】如图,正方体 ![]() 的棱长为1,
的棱长为1, ![]() 分别是棱
分别是棱 ![]() 的中点,过
的中点,过 ![]() 的平面与棱
的平面与棱 ![]() 分别交于点
分别交于点 ![]() .设
.设 ![]() ,
, ![]() .
.
①四边形 ![]() 一定是菱形;②
一定是菱形;② ![]() 平面
平面 ![]() ;③四边形
;③四边形 ![]() 的面积
的面积 ![]() 在区间
在区间 ![]() 上具有单调性;④四棱锥
上具有单调性;④四棱锥 ![]() 的体积为定值.
的体积为定值.
以上结论正确的个数是( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,给出以下四个命题:
,给出以下四个命题:
① ![]() ,有
,有 ![]() ;
;
② ![]() 且
且 ![]() ,有
,有 ![]() ;
;
③ ![]() ,有
,有 ![]() ;
;
④ ![]() ,
, ![]() .
.
其中所有真命题的序号是( )
A.①②
B.③④
C.①②③
D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com