
【题目】在平面直角坐标系xOy中,已知定点A(-4,0)、C(4,0),半径为r的圆M的圆心M在线段AC的垂直平分线上,且在y轴右侧,圆M被y轴截得的弦长为![]() r.
r.
(1)求圆M的方程;(2)当r变化时,是否存在定直线l与动圆M均相切?如果存在,求出定直线l的方程;如果不存在,说明理由.
【答案】(1)![]() ;(2) 存在两条直线y=3和4x+3y-9=0与动圆M均相切.
;(2) 存在两条直线y=3和4x+3y-9=0与动圆M均相切.
【解析】试题分析:(1)根据圆心在弦的中垂线上求得线段AC的垂直平分线方程为y=2x+3,可知圆心在这条线上,设圆心为M(a,2a+3)再有垂径定理构造方程求解即可;(2)由直线和圆相切的性质得到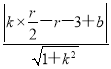 =r,圆心到直线的距离为半径,再根据方程恒等得到
=r,圆心到直线的距离为半径,再根据方程恒等得到
对应系数相等即可;
(1)由题意C(0,-2),A(-4,0),
所以线段AC的垂直平分线方程为y=2x+3.
设M(a,2a+3)(a>0),则圆M的方程为(x-a)2+(y-2a-3)2=r2.
圆心M到y轴的距离d=a,由r2=d2+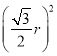 ,得a=
,得a=![]() .
.
所以圆M的方程为![]() +(y-r-3)2=r2.
+(y-r-3)2=r2.
(2)假设存在定直线l与动圆M均相切.当定直线的斜率不存在时,不合题意.
设直线l:y=kx+b,则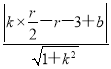 =r对任意r>0恒成立.
=r对任意r>0恒成立.
由![]() ,得
,得![]() r2+(k-2)(b-3)r+(b-3)2=(1+k2)r2.
r2+(k-2)(b-3)r+(b-3)2=(1+k2)r2.
所以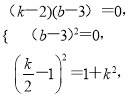 解得
解得![]() 或
或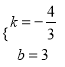
所以存在两条直线y=3和4x+3y-9=0与动圆M均相切.


科目:高中数学 来源: 题型:
【题目】为了了解2013年某校高三学生的视力情况,随机抽查了一部分学生视力,将调查结果分组,分组区间为![]() ,
,![]() ,… ,
,… ,![]() 经过数据处理,得到如右频率分布表:
经过数据处理,得到如右频率分布表:
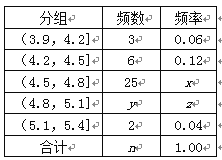
(1)求频率分布表中未知量![]() 的值;
的值;
(2)从样本中视力在![]() 和
和![]() 的所有同学中随机抽取两人,求两人的视力差的绝对值低于0.5的概率.
的所有同学中随机抽取两人,求两人的视力差的绝对值低于0.5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区拟建立一个艺术博物馆,采取竞标的方式从多家建筑公司选取一家建筑公司,经过层层筛选,甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从![]() 个招标问题中随机抽取
个招标问题中随机抽取![]() 个问题,已知这
个问题,已知这![]() 个招标问题中,甲公司可正确回答其中的
个招标问题中,甲公司可正确回答其中的![]() 道題目,而乙公司能正确回答毎道题目的概率均为
道題目,而乙公司能正确回答毎道题目的概率均为![]() ,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
(1)求甲、乙两家公司共答对![]() 道题目的概率;
道题目的概率;
(2)请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 中,各棱长均为6,
中,各棱长均为6, ![]() 分别是侧棱
分别是侧棱![]() 、
、![]() 上的点,且
上的点,且![]() .
.
(1)在![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?证明你的结论;
?证明你的结论;
(2)求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某书店销售刚刚上市的某知名品牌的高三数学单元卷,按事先拟定的价格进行5天试销,每种单价试销1天,得到如表数据:
单价x(元) | 18 | 19 | 20 | 21 | 22 |
销量y(册) | 61 | 56 | 50 | 48 | 45 |
(1)求试销5天的销量的方差和y对x的回归直线方程;
(2)预计今后的销售中,销量与单价服从(1)中的回归方程,已知每册单元卷的成本是14元,
为了获得最大利润,该单元卷的单价应定为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年被业界称为![]() (虚拟现实技术)元年,未来
(虚拟现实技术)元年,未来![]() 技术将给教育、医疗、娱乐、商业、交通旅游等多领域带来极大改变,某
技术将给教育、医疗、娱乐、商业、交通旅游等多领域带来极大改变,某![]() 教育设备生产企业有甲、乙两类产品,其中生产一件甲产品需
教育设备生产企业有甲、乙两类产品,其中生产一件甲产品需![]() 团队投入15天时间,
团队投入15天时间, ![]() 团队投入20天时间,总费用10万元,甲产品售价为15万元/件;生产一件乙产品需
团队投入20天时间,总费用10万元,甲产品售价为15万元/件;生产一件乙产品需![]() 团队投入20天时间,
团队投入20天时间, ![]() 团队投入16天时间,总费用15万元,乙产品售价为25万元/件,
团队投入16天时间,总费用15万元,乙产品售价为25万元/件, ![]() 、
、![]() 两个团队分别独立运作.现某客户欲以不超过200万元订购该企业甲、乙两类产品,要求每类产品至少各3件,在期限180天内,为使企业总效益最佳,则最后交付的甲、乙两类产品数之和为__________.
两个团队分别独立运作.现某客户欲以不超过200万元订购该企业甲、乙两类产品,要求每类产品至少各3件,在期限180天内,为使企业总效益最佳,则最后交付的甲、乙两类产品数之和为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过点
经过点![]() ,
, ![]() ,并且直线
,并且直线![]() 平分圆
平分圆![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 交于
交于![]() 两点,是否存在直线
两点,是否存在直线![]() ,使得
,使得![]() (
(![]() 为坐标原点),若存在,求出
为坐标原点),若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(Ⅰ)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设曲线![]() 经过伸缩变换
经过伸缩变换 得到曲线
得到曲线![]() ,若点
,若点![]() ,直线
,直线![]() 与
与![]() 交与
交与![]() ,
, ![]() ,求
,求![]() ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com