【题目】甲乙两人参加竞选，结果是甲得
票，乙得
票
. 试求：唱票中甲累计的票数始终超过乙累计的票数的概率.
【答案】
【解析】
若唱甲当选，则记为1；若唱乙当选，则记为
. 每一种唱票方式都对应一个由
个1和
个组成的排列. 用
表示谴责
项的和，在直角坐标系中标出点
，并将点与点
用线段联结
. 这样，每一种唱票方式都对应一条联结
与
的折线. 而甲累计的票数始终领先等价于所有的点都在
轴的上方，即折线与轴无交点（我们称为“好折线”，反之为“坏折线”）.
显然，联结
、
的“自由”（无限定条件）折线有
条，这是因为在
段中选择段为上升有种方法.
对每一条坏折线，有如下两种情形：一是经过点
，二是经过点
.
对于第一种情形，坏折线是由
到的自由折线，从而，这样的折线有
条.
对于第二种情形，注意到过的坏折线必与轴相交，设其横坐标最小的交点为
. 将此折线位于左边的部分作关于轴的对称折线，便得到过点的坏折线，于是，坏折线的条数也有条. 所以，合乎条件的好折线的条数为
.
综上所述，所求的概率为
.
科目：高中数学 来源： 题型：
【题目】南昌市在2018年召开了全球VR产业大会，为了增强对青少年VR知识的普及，某中学举行了一次普及VR知识讲座，并从参加讲座的男生中随机抽取了50人，女生中随机抽取了70人参加VR知识测试，成绩分成优秀和非优秀两类，统计两类成绩人数得到如下的
列联表：
优秀 | 非优秀 | 总计 | |
男生 |
| 35 | 50 |
女生 | 30 |
| 70 |
总计 | 45 | 75 | 120 |
（1）确定
，
的值；
（2）试判断能否有90%的把握认为VR知识测试成绩优秀与否与性别有关；
附：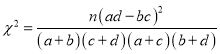
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在正方体
中，点E是棱
的中点，点F是线段
上的一个动点．有以下三个命题：
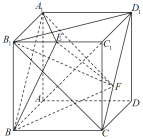
①异面直线
与
所成的角是定值；
②三棱锥
的体积是定值；
③直线
与平面
所成的角是定值．
其中真命题的个数是( )
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某种出口产品的关税税率t．市场价格x(单位：千元)与市场供应量p(单位：万件)之间近似满足关系式：
，其中k．b均为常数．当关税税率为75%时，若市场价格为5千元，则市场供应量约为1万件；若市场价格为7千元，则市场供应量约为2万件．
(1)试确定k．b的值；
(2)市场需求量q(单位：万件)与市场价格x近似满足关系式：
．P = q时，市场价格称为市场平衡价格．当市场平衡价格不超过4千元时，试确定关税税率
的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线C：
的焦点坐标为
，点
，过点P作直线l交抛物线C于A，B两点，过A，B分别作抛物线C的切线，两切线交于点Q，且两切线分别交x轴于M，N两点，则
面积的最小值为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线
的焦点为
，准线为
，抛物线
上存在一点
，过点作
，垂足为
，使
是等边三角形且面积为
.
（1）求抛物线的方程；
（2）若点
是圆
与抛物线的一个交点，点
，当
取得最小值时，求此时圆
的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】有5名同学进行投篮比赛，决出第1名至第5名的不同名次，教练在公布成绩前透露，五名同学中的甲乙名次相邻，丙不是第一名，丁不是最后一名，根据教练的说法，这5名同学的名次排列最多有（ ）种不同的情况.
A.28B.32C.54D.64
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图
，梯形
中，
，过
分别作
，
，垂足分别
，
，已知
，将梯形沿
同侧折起，得空间几何体
，如图
．
1
若
，证明：
平面
；
2若
，
，线段
上存在一点
，满足
与平面
所成角的正弦值为
，求
的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
