
分析 (1)设出直线的方程与抛物线方程联立消去y,设直线l与抛物线两个不同的交点坐标为A,B,进而根据判别是对大于0,及x1+x2的和x1x2的表达式,求得AB的长度的表达式,根据|AB|的范围确定a的范围
(2)求出线段AB的垂直平分线方程,得Q的坐标,进而表示出△NAB的面积,根据|AB|范围确定三角形面积的最大值.
解答 解:(1)设直线l的方程为y=x-m代入y2=ax,
得y2-ay-am=0.
设直线l与抛物线两个不同的交点坐标为A(x1,y1)、B(x2,y2),
△=a2-4(-am)>0,∴m>-$\frac{a}{4}$,
y1+y2=a,y1y2=-am,
|AB|=$\sqrt{2}•$$\sqrt{({a}^{2}+4am)}$≤a,∴m$≤-\frac{a}{8}$,
∴-$\frac{a}{4}$<m$≤-\frac{a}{8}$;
(2)由(1)线段AB的中点坐标为($\frac{a}{2}$+m,$\frac{a}{2}$),
线段AB的垂直平分线方程为y-$\frac{a}{2}$=-(x-$\frac{a}{2}$-m),
令y=0,可得Q(m+a,0),
Q到AB的距离d=$\frac{a}{\sqrt{2}}$,
∴△QAB面积S=$\frac{1}{2}•\frac{a}{\sqrt{2}}•|AB|$≤$\frac{1}{2}•\frac{a}{\sqrt{2}}•a$=$\frac{\sqrt{2}}{4}{a}^{2}$,
∴△QAB面积的最大值为$\frac{\sqrt{2}}{4}{a}^{2}$.
点评 本小题考查直线与抛物线的基本概念及位置关系,考查运用解析几何的方法解决数学问题的能力.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:解答题
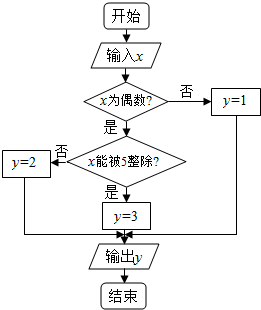 某算法的程序框图如图所示,其中输入的变量J在1,2,3,…,30这30个整数中等可能随机产生.
某算法的程序框图如图所示,其中输入的变量J在1,2,3,…,30这30个整数中等可能随机产生.| 运行次数 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
| 30 | 16 | 11 | 3 |
| … | … | … | … |
| 2000 | 967 | 783 | 250 |
| 运行次数 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
| 30 | 13 | 13 | 4 |
| … | … | … | … |
| 2000 | 998 | 803 | 199 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 椭圆的一部分 | B. | 双曲线的一部分 | C. | 抛物线的一部分 | D. | 圆的一部分 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 分层抽样 | B. | 抽签法 | C. | 随机数表法 | D. | 系统抽样法 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | $-\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com