
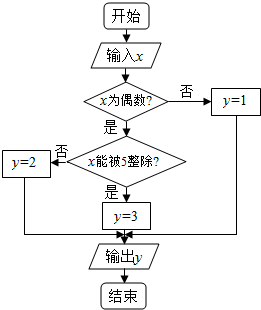
 某算法的程序框图如图所示,其中输入的变量J在1,2,3,…,30这30个整数中等可能随机产生.
某算法的程序框图如图所示,其中输入的变量J在1,2,3,…,30这30个整数中等可能随机产生.| 运行次数 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
| 30 | 16 | 11 | 3 |
| … | … | … | … |
| 2000 | 967 | 783 | 250 |
| 运行次数 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
| 30 | 13 | 13 | 4 |
| … | … | … | … |
| 2000 | 998 | 803 | 199 |
分析 (1)由题意可得,变量x是从1,2,3,…30这30个整数中可能随机产生的一个数,共有30中结果,当变量x从1,3,5,7,9,11,13,15,17,19,21,23,25,27,29这15个整数中产生时,输出y的值为1,所以P1=$\frac{1}{2}$,当变量x从2,4,6,8,12,14,16,18,22,24,26,28这12个整数中产生时,输出原点值为2,所以P2=$\frac{2}{5}$,当变量x从10,20,30这3个整数中产生时,输出y的值为3,所以P3=$\frac{1}{10}$.…
(2)当n=2000时,列出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率的表格,再比较频率趋势与概率,即可得解.
解答 (本题满分10分)
解:(1)由题意可得,变量x是从1,2,3,…30这30个整数中可能随机产生的一个数,共有30中结果,
当变量x从1,3,5,7,9,11,13,15,17,19,21,23,25,27,29这15个整数中产生时,输出y的值为1,所以P1=$\frac{1}{2}$,
当变量x从2,4,6,8,12,14,16,18,22,24,26,28这12个整数中产生时,输出原点值为2,所以P2=$\frac{2}{5}$,
当变量x从10,20,30这3个整数中产生时,输出y的值为3,所以P3=$\frac{1}{10}$.…6分
(2)当n=2000时,甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率如下,
| n=2000 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
| 甲 | $\frac{967}{2000}$ | $\frac{783}{2000}$ | $\frac{1}{8}$ |
| 乙 | $\frac{499}{1000}$ | $\frac{803}{2000}$ | $\frac{199}{2000}$ |
点评 本题综合考查程序框图、古典概型及其概率计算公式等基础知识,考查运算求解能力,属于基础题.


 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源: 题型:解答题
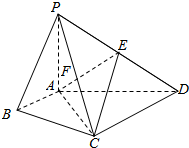 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=4.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -8 | B. | -6 | C. | 0 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{10}{3}$ | C. | $\frac{20}{3}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 长轴长 | B. | 短轴长 | C. | 焦距 | D. | 离心率 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com