
| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{10}{3}$ | C. | $\frac{20}{3}$ | D. | $\frac{5}{3}$ |
分析 求出椭圆的焦点坐标,结合椭圆的定义,通过三角形的面积转化求解即可.
解答 解:椭圆:$\frac{x^2}{25}+\frac{y^2}{16}=1$,a=5,b=4,∴c=3,左、右焦点F1(-3,0)、F2( 3,0),
△ABF2的内切圆面积为π,则内切圆的半径为r=$\frac{1}{2}$,
而△ABF2的面积=△A F1F2的面积+△BF1F2的面积=$\frac{1}{2}$×|y1|×|F1F2|+$\frac{1}{2}$×|y2|×|F1F2|=$\frac{1}{2}$×(|y1|+|y2|)×|F1F2|=3|y2-y1|(A、B在x轴的上下两侧)
又△ABF2的面积=$\frac{1}{2}$×r(|AB|+|BF2|+|F2A|)=$\frac{1}{2}×\frac{1}{2}$(2a+2a)=a=5.
所以 3|y2-y1|=5,|y2-y1|=$\frac{5}{3}$.
故选:D.
点评 本题考查椭圆的简单性质的应用,考查计算能力以及转化思想的应用


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | l3⊥l4 | B. | l3∥l4 | ||
| C. | l3,l4既不平行也不垂直 | D. | l3,l4的位置关系不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
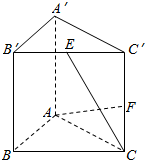 在直三棱柱ABC-A′B′C′中,AB=AC=2,AA′=3,AB⊥AC,E为棱B′C′的中点,F为侧棱CC′上一点,若CE⊥AF,则AF与平面ABB′A′所成的角的正切值为( )
在直三棱柱ABC-A′B′C′中,AB=AC=2,AA′=3,AB⊥AC,E为棱B′C′的中点,F为侧棱CC′上一点,若CE⊥AF,则AF与平面ABB′A′所成的角的正切值为( )| A. | 3 | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
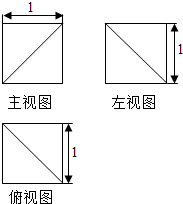
| A. | $\frac{{9+\sqrt{3}}}{2}$ | B. | 5 | C. | $\frac{{18+\sqrt{3}}}{4}$ | D. | $4+\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
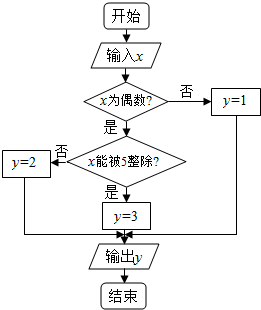 某算法的程序框图如图所示,其中输入的变量J在1,2,3,…,30这30个整数中等可能随机产生.
某算法的程序框图如图所示,其中输入的变量J在1,2,3,…,30这30个整数中等可能随机产生.| 运行次数 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
| 30 | 16 | 11 | 3 |
| … | … | … | … |
| 2000 | 967 | 783 | 250 |
| 运行次数 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
| 30 | 13 | 13 | 4 |
| … | … | … | … |
| 2000 | 998 | 803 | 199 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 椭圆的一部分 | B. | 双曲线的一部分 | C. | 抛物线的一部分 | D. | 圆的一部分 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com