
已知函数f(x)满足2f(x+2)=f(x),当x∈(0,2)时,f(x)=lnx+ax ( ),当x∈(―4,―2)时,f(x)的最大值为―4.
),当x∈(―4,―2)时,f(x)的最大值为―4.
(1)求x∈(0,2)时,f(x)的解析式;
(2)是否存在实数b使得不等式 对于
对于 恒成立?若存在,求出实数b的取值集合;若不存在,请说明理由.
恒成立?若存在,求出实数b的取值集合;若不存在,请说明理由.
(1)f(x)=lnx-x;(2){1}
【解析】试题分析:(1)由已知得:f(x)=2f(x+2)=4f(x+4),设x∈(-4,-2)时,则x+4∈(0,2),代入x∈(0,2)时,f(x)=lnx+ax(a<?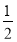 ),求出f(x+4)=ln(x+4)+a(x+4),再根据当x∈(-4,-2)时,f(x)的最大值为-4,利用导数求得它的最大值,解方程即可求得a的值,进而求得结论;
),求出f(x+4)=ln(x+4)+a(x+4),再根据当x∈(-4,-2)时,f(x)的最大值为-4,利用导数求得它的最大值,解方程即可求得a的值,进而求得结论;
(2)假设存在实数b使得不等式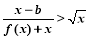 对于x∈(0,1)∪(1,2)时恒成立,由(1)可得:x∈(0,1)∪(1,2)时,不等式
对于x∈(0,1)∪(1,2)时恒成立,由(1)可得:x∈(0,1)∪(1,2)时,不等式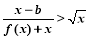 恒成立,利用分离参数的方法,转化为求函数的最值问题,即可求得b的值.
恒成立,利用分离参数的方法,转化为求函数的最值问题,即可求得b的值.
试题解析:(1)由已知,f(x)=2f(x+2)=4f(x+4)
当x∈(0,2)时,f(x)=lnx+ax(a<-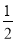 )
)
当x∈(-4,-2)时,x+4∈(0,2),
∴f(x+4)=ln(x+4)+a(x+4)
∴当x∈(-4,-2)时,f(x)=4f(x+4)=4ln(x+4)+4a(x+4)
∴f '(x)= +4a=4a•
+4a=4a• ,
,
∵a<?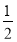 ,∴?4<?
,∴?4<?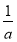 ?4<?2,
?4<?2,
∴当x∈(?4, ?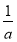 ?4)时,f′(x)>0,f(x)为增函数,
?4)时,f′(x)>0,f(x)为增函数,
当x∈(?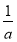 ?4,?2)时,f′(x)<0,f(x)为减函数,
?4,?2)时,f′(x)<0,f(x)为减函数,
∴f(x)max=f(?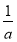 ?4)=4ln(?
?4)=4ln(?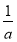 )+4a(?
)+4a(?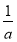 )=?4,∴a=-1
)=?4,∴a=-1
∴当x∈(0,2)时,f(x)=lnx-x
(2)由(1)可得:x∈(0,1)∪(1,2)时,不等式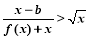 恒成立,
恒成立,
即为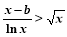 恒成立,
恒成立,
①当x∈(0,1)时,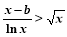
⇒b>x?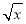 lnx,令g(x)=x?
lnx,令g(x)=x?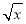 lnx,x∈(0,1)
lnx,x∈(0,1)
则g′(x)=1?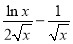 =
=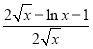
令h(x)=2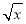 ?lnx?2,
?lnx?2,
则当x∈(0,1)时,h′(x)=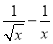 =
=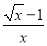 <0
<0
∴h(x)>h(1)=0,∴g′(x)= >0,
>0,
∴g(x)<g(1)=1,故此时只需b≥1即可;
②当x∈(1,2)时,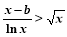
⇒b<x?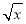 lnx,令φ(x)=x?
lnx,令φ(x)=x?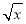 lnx,x∈(1,2)
lnx,x∈(1,2)
则φ′(x)=1?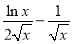 =
=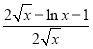
令h(x)=2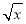 ?lnx?2,
?lnx?2,
则当x∈(1,2)时,h′(x)=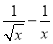 =
=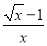 >0
>0
∴h(x)>h(1)=0,∴φ′(x)= >0,
>0,
∴φ(x)>φ(1)=1,故此时只需b≤1即可,
综上所述:b=1,因此满足题中b的取值集合为:{1}
考点:利用导数研究函数的单调性,最值,函数的周期性,不等式恒成立问题,分类讨论.


科目:高中数学 来源: 题型:
| π |
| 4 |
| 2 |
|
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试理科数学试卷(解析版) 题型:选择题
△ABC中,|AB|=10,|AC|=15,∠BAC= ,点D是边AB的中点,点E在直线AC上,且
,点D是边AB的中点,点E在直线AC上,且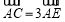 ,直线CD与BE相交于点P,则线段AP的长为( )
,直线CD与BE相交于点P,则线段AP的长为( )
A.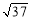 B.
B.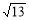 C.2
C.2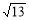 D.2
D.2
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试文科数学试卷(解析版) 题型:填空题
已知函数f(x)是定义域为R的奇函数,且周期为2,若当x∈[0,1)时,f(x)=2x-1,则f(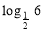 )的值是________________.
)的值是________________.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试文科数学试卷(解析版) 题型:选择题
设f(x)=4sinxsin +cos2x,|f(x)-m|<3对?x∈R恒成立,则实数m的范围是( )
+cos2x,|f(x)-m|<3对?x∈R恒成立,则实数m的范围是( )
A.(0,2] B.[0,2] C.[0,2) D.(0,2)
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考理科数学试卷(解析版) 题型:解答题
已知向量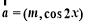 ,
,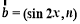 ,函数f(x)=
,函数f(x)=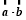 ,且y=f(x)的图象过点
,且y=f(x)的图象过点 和点
和点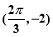 .
.
(1)求m,n的值;
(2)将y=f(x)的图象向左平移φ(0<φ<π)个单位后得到函数y=g(x)的图象,若y=g(x)图象上各最高点到点(0,3)的距离的最小值为1,求y=g(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考理科数学试卷(解析版) 题型:选择题
已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)= (|x-a2|+|x-2a2|-3a2).若?x∈R,f(x-1)≤f(x),则实数a的取值范围为( )
(|x-a2|+|x-2a2|-3a2).若?x∈R,f(x-1)≤f(x),则实数a的取值范围为( )
A.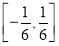 B.
B. C.
C.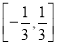 D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考文科数学试卷(解析版) 题型:填空题
已知圆x2+y2+mx-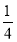 =0与抛物线y=
=0与抛物线y=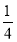 x2的准线相切,则m= _________ .
x2的准线相切,则m= _________ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com