
| π |
| 4 |
| 2 |
|
| π |
| 4 |
| 2 |
| π |
| 4 |
| 2 |
|
| 1 | ||
|
| ||
| 2 |
| r2-d2 |
16-
|
| 62 |
| 62 |
| 62 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| 2 |
| π |
| 4 |
|
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考理科数学试卷(解析版) 题型:解答题
已知函数f(x)满足2f(x+2)=f(x),当x∈(0,2)时,f(x)=lnx+ax ( ),当x∈(―4,―2)时,f(x)的最大值为―4.
),当x∈(―4,―2)时,f(x)的最大值为―4.
(1)求x∈(0,2)时,f(x)的解析式;
(2)是否存在实数b使得不等式 对于
对于 恒成立?若存在,求出实数b的取值集合;若不存在,请说明理由.
恒成立?若存在,求出实数b的取值集合;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考文科数学试卷(解析版) 题型:选择题
如图所示的韦恩图中,阴影部分对应的集合是( )
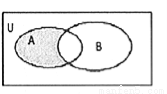
A.A∩B B.?U(A∩B) C.A∩(?UB) D.(?UA)∩B
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都实验外国语高三11月月考理科数学试卷(解析版) 题型:选择题
某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的表面积为( )
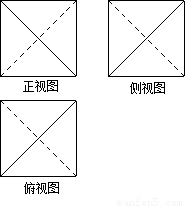
A.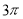 B.
B.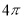 C.
C.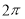 D.
D.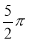
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com