
分析 (1)分a>0和a≤0两种情况讨论,可得原不等式的解集;
(2)f(x+1)+f(2x)≤4可化为:$\left\{\begin{array}{l}x≤-1\\-3x-1≤4\end{array}\right.$,或$\left\{\begin{array}{l}-1<x<0\\ 1-x≤4\end{array}\right.$,或$\left\{\begin{array}{l}x≥0\\ 3x+1≤4\end{array}\right.$,解得答案.
解答 解:(1)若a>0,不等式f(x-1)<a可化为:|x-1|<a,解得1-a<x<1+a;
故原不等式的解集为:(1-a,1+a);
若a≤0,则不等式f(x-1)<a的解集为∅…(4分)
(2)由f(x+1)+f(2x)≤4得:
|x+1|+|2x|≤4
∴原问题等价于|x+1|+|2x|≤4,
∴$\left\{\begin{array}{l}x≤-1\\-3x-1≤4\end{array}\right.$,或$\left\{\begin{array}{l}-1<x<0\\ 1-x≤4\end{array}\right.$,或$\left\{\begin{array}{l}x≥0\\ 3x+1≤4\end{array}\right.$
解得:-$\frac{5}{3}$≤x≤1.
故原不等式的解集为:[-$\frac{5}{3}$,1]…(10分)
点评 本题考查的知识点是分段函数的应用,分类讨论思想,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
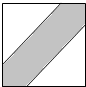 如图,在边长为25cm的正方形中挖去边长为23cm的两个等腰直角三角形,现有均匀的粒子散落在正方形中,问粒子落在中间阴影区域的概率是( )
如图,在边长为25cm的正方形中挖去边长为23cm的两个等腰直角三角形,现有均匀的粒子散落在正方形中,问粒子落在中间阴影区域的概率是( )| A. | $\frac{529}{625}$ | B. | $\frac{96}{625}$ | C. | $\frac{23}{25}$ | D. | $\frac{2}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<a<1 | B. | 0≤a≤1 | C. | 0<a≤1 | D. | 0≤a<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{5}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com