
【题目】已知函数![]() .
.
(1) 求![]() 的单调区间;
的单调区间;
(2) 讨论![]() 在
在![]() 上的零点个数.
上的零点个数.
【答案】(1)见解析(2)见解析
【解析】试题分析:
(1)求导数得![]() ,当
,当![]() 时,则
时,则![]() 恒成立,故
恒成立,故![]() 的单调递増区间为
的单调递増区间为![]() .当
.当![]() 时,由
时,由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
故![]() 的单调递増区间为
的单调递増区间为![]() ,单调递减区间为
,单调递减区间为![]() .(2)令
.(2)令![]() ,分离参数得
,分离参数得![]() ,由于
,由于![]() ,故当
,故当![]() 时,函数
时,函数![]() 无零点;当
无零点;当![]() 时,令
时,令![]() ,可得
,可得![]() 在
在![]() 上单调递增,在(
上单调递增,在(![]() 上单调递减,故
上单调递减,故![]() ,所以当
,所以当![]() 时,
时, ![]() 有1个零点,当
有1个零点,当![]() 时,
时, ![]() 有2个零点.
有2个零点.
试题解析:
⑴因为![]() ,
,
所以![]() ,
,
①当![]() 时,则
时,则![]() 恒成立,
恒成立,
所以![]() 的单调递増区间为
的单调递増区间为![]() ,
,
②当![]() 时,
时,
令![]() 得
得![]() ,
,
令![]() 得
得![]() ,
,
所以![]() 的单调递増区间为
的单调递増区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
综上:当![]() 时,
时, ![]() 的单调递増区间为
的单调递増区间为![]() ;
;
当![]() 时,
时, ![]() 的单调递増区间为
的单调递増区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)令![]() ,
,
所以![]()
因为![]() ,所以
,所以![]() ,
,
所以若![]() ,则
,则![]() 无零点.
无零点.
若![]() ,令
,令![]() ,
,
则![]() ,
,
故当![]() 时,
时, ![]() ,
, ![]() 单调递增;当
单调递增;当![]() 时,
时, ![]() ,
, ![]() 单调递减.
单调递减.
所以当![]() 时,
时, ![]() 有极大值,也为最大值,且
有极大值,也为最大值,且![]() ,
,
又当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
所以当![]() 时,
时, ![]() 有1个零点,
有1个零点,
当![]() 时,
时, ![]() 有2个零点.
有2个零点.
综上,当![]() 时,函数
时,函数![]() 无零点;当
无零点;当![]() 时,
时, ![]() 有1个零点;当
有1个零点;当![]() 时,
时, ![]() 有2个零点.
有2个零点.


科目:高中数学 来源: 题型:
【题目】A、B两人进行一局围棋比赛,A获得的概率为0.8,若采用三局两胜制举行一次比赛,现采用随机模拟的方法估计B获胜的概率.先利用计算器或计算机生成0到9之间取整数值的随机数,用0,1,2,3,4,5,6,7表示A获胜;8,9表示B获胜,这样能体现A获胜的概率为0.8.因为采用三局两胜制,所以每3个随机数作为一组.
例如,产生30组随机数:034 743 738 636 964 736 614 698 637 162 332 616 804 560 111 410 959 774 246 762 428 114 572 042 533 237 322 707 360 751,据此估计B获胜的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有6个球,其中4个白球,2个红球,从袋中任意取出两球,求下列事件的概率:
(1) 取出的两球1个是白球,另1个是红球;
(2) 取出的两球至少一个是白球。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域为![]() 的函数
的函数![]() 满足:
满足:![]() ,且对于任意实数
,且对于任意实数![]() ,
,![]() 恒有
恒有![]() ,当
,当![]() 时,
时,![]() .
.
(1)求![]() 的值,并证明当
的值,并证明当![]() 时,
时,![]() ;
;
(2)判断函数![]() 在
在![]() 上的单调性并加以证明;
上的单调性并加以证明;
(3)若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018届广东省汕头市高三上学期期末】某大型企业为鼓励员工多利用网络进行营销,准备为员工办理手机流量套餐.为了解员工手机流量使用情况,通过抽样,得到100位员工每人手机月平均使用流量![]() (单位:
(单位: ![]() )的数据,其频率分布直方图如下:
)的数据,其频率分布直方图如下:
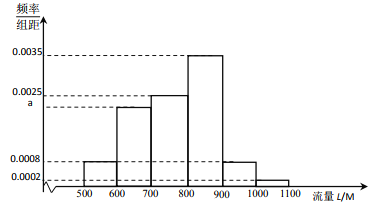
将频率视为概率,同一组中的数据用该组区间的中点值代替,回答以下问题:
(1) 求出![]() 的值,并计算这100位员工每月手机使用流量的平均值;
的值,并计算这100位员工每月手机使用流量的平均值;
(2) 据了解,某网络营运商推出两款流量套餐,详情如下:

流量套餐的规则是:每月1日收取套餐费。如果手机实际使用流量超出套餐流量,则需要购买流量叠加包,每一个叠加包(包含![]() 的流量)需要10元,可以多次购买;如果当月流量有剩余,将会被清零.
的流量)需要10元,可以多次购买;如果当月流量有剩余,将会被清零.
该企业准备订购其中一款流量套餐,每月为员工支付套餐费,以及购买流量叠加包所需月费用.若以平均费用为决策依据,该企业订购哪一款套餐更经济?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为1, 圆心在
的半径为1, 圆心在![]() 上.
上.

(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线方程;
的切线,求切线方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某翻译处有8名翻译,其中有小张等3名英语翻译,小李等3名日语翻译,另外2名既能翻译英语又能翻译日语,现需选取5名翻译参加翻译工作,3名翻译英语,2名翻译日语,且小张与小李恰有1人选中,则有____种不同选取方法.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求适合下列条件的双曲线的标准方程:
(1)过点(3,-![]() ),离心率e=
),离心率e=![]() ;
;
(2)中心在原点,焦点F1,F2在坐标轴上,实轴长和虚轴长相等,且过点P(4,-![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,PA![]() 平面ABCD,EB//PA,AB=PA=4,EB=2,F为PD的中点.
平面ABCD,EB//PA,AB=PA=4,EB=2,F为PD的中点.
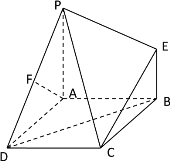
(1)求证AF![]() PC
PC
(2)BD//平面PEC
(3)求二面角D-PC-E的大小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com