练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．如图是某种可固定在墙上的广告金属支架模型，其中AD=6，C是AB的中点，∠BCD=$\frac{π}{3}$，∠BAD=θ（θ∈（$\frac{π}{9}$，$\frac{π}{3}$）
    （Ⅰ）若θ=$\frac{π}{4}$，求AB的长；
    （Ⅱ） 求BD的长f（θ），并求f（θ）的最小值；
    （Ⅲ） 经市场调查发现，某地对该种金属支架的需求量与θ有关，且需求量g（θ）的函数关系式为g（θ）=4sin6θ+6θ（单位：万件），试探究是否存在某种规格的金属支架在当地需求量为零？并说明理由．

    分析 （Ⅰ）若θ=$\frac{π}{4}$，由正弦定理得AC，即可求AB的长；
    （Ⅱ）由余弦定理得BD的长f（θ），利用三角函数的性质，即可求f（θ）的最小值；
    （Ⅲ）设x=6θ，x∈（$\frac{2π}{3}$，2π），令h（x）=4sinx+x，问题转化为在（$\frac{2π}{3}$，2π）是否存在x的值，使是h（x）=0，分类讨论可得结论．

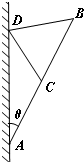    解答 解：（Ⅰ）在△ACD中，已知AD=6，∠ACD=$\frac{2π}{3}$，∠ADC=$\frac{π}{3}$-θ，
    由正弦定理得：$\frac{AC}{sin（\frac{π}{3}-θ）}=\frac{AD}{sin\frac{2π}{3}}$，
    故AC=4$\sqrt{3}$sin（$\frac{π}{3}$-θ）．…（2分）
    当θ=$\frac{π}{4}$时，AC=4$\sqrt{3}$sin（$\frac{π}{3}$-$\frac{π}{4}$）=4$\sqrt{3}$•$\frac{\sqrt{6}-\sqrt{2}}{4}$=3$\sqrt{2}$-$\sqrt{6}$
    故AB的长为6$\sqrt{2}$-2$\sqrt{6}$．　　　                         …（4分）
    （Ⅱ）在△ABD中，已知AD=6，AB=8$\sqrt{3}$sin（$\frac{π}{3}$-θ），∠BAD=θ，
    由余弦定理得：BD2=AD2+AB2-2AD•AB•cosθ　　　                  …（5分）
    =36+[8$\sqrt{3}$sin（$\frac{π}{3}$-θ）]2-24×4$\sqrt{3}$sin（$\frac{π}{3}$-θ）cosθ
    =60-48sin（2θ+$\frac{π}{6}$）　                    …（7分）
    因为θ∈（$\frac{π}{9}$，$\frac{π}{3}$），所以2θ+$\frac{π}{6}$∈（$\frac{7π}{18}$，$\frac{5π}{6}$），即sin（2θ+$\frac{π}{6}$）≤1
    所以BD≥$\sqrt{60-48}$=2$\sqrt{3}$，
    则BD的最小值为2$\sqrt{3}$，此时sin（2θ+$\frac{π}{6}$）=1，即θ=$\frac{π}{6}$．…（9分）
    （Ⅲ）设x=6θ，x∈（$\frac{2π}{3}$，2π），令h（x）=4sinx+x，
    问题转化为在（$\frac{2π}{3}$，2π）是否存在x的值，使是h（x）=0，…（10分）
    ①当x∈（4，2π）时，|sinx|≤1，必有h（x）=4sinx+x＞0；
    ②当x∈（$\frac{2π}{3}$，4]时，h′（x）=4cosx+1＜0，在x∈（$\frac{2π}{3}$，$\frac{4π}{3}$）恒成立，h（x）在区间（$\frac{2π}{3}$，$\frac{4π}{3}$）递减，
    于是h（x）≥h（4）＞h（$\frac{4π}{3}$）=4sin$\frac{4π}{3}$+$\frac{4π}{3}$＞-2$\sqrt{3}$+4＞0
    综上，在 （$\frac{2π}{3}$，2π），h（x）＞0恒成立，故不存在某种规格的金属支架，在当地需求量为零．…（13分）

    点评 本题考查解三角形的运用，考查三角函数知识，考查分类讨论的数学思想，考查学生分析解决问题的能力，难度大．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    20．已知函数f（x）=2cos2x+$\sqrt{3}$sin2x-1．
    （1）将函数f（x）化为Asin（ωx+φ）的形式；
    （2）求函数的最大值及最小正周期．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知圆锥曲线mx2+y2=1的离心率为$\sqrt{2}$，则实数m的值为（　　）
    A．-1B．-2C．-3D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．若经过点P（-3，0）的直线l与圆M：x2+y2+4x-2y+3=0相切，则圆M的圆心坐标是（-2，1）；半径为$\sqrt{2}$；切线在y轴上的截距是-3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．设平面α与平面β相交于直线m，直线l1在平面α内，直线l2在平面β内，且l2⊥m，则“l1⊥l2”是“α⊥β”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充分必要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．在△ABC中，∠ABC=30°，AB=$\sqrt{3}$，BC边上的中线AD=1，则AC的长度为（　　）
    A．1或$\sqrt{7}$B．$\sqrt{7}$C．$\sqrt{3}$D．1或$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．已知数列{an}是公比大于1的等比数列，其前n项和为Sn，且a1，a3是方程x2-5x+4=0的两根，则S3=7．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．某校计划组织高一年级四个班开展研学旅行活动，初选了A，B，C，D四条不同的研学线路，每个班级只能在这四条线路中选择其中的一条，且同一线路最多只能有两个班级选择，则不同的选择方案有（　　）
    A．240种B．204种C．188种D．96种

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知函数f（x）=lnx-x-lna（x＞0），其中a＞0
    （1）求函数h（x）=f（x）+$\frac{1}{2}{x^2}$-ax+（a-1）lnx的单调递增区间；
    （2）若函数f（x）有两个零点x1，x2，且x1＜x2，求实数a的取值范围，并证明$\frac{x_2}{x_1}$随a的增大而减小．

    查看答案和解析>>

    同步练习册答案