
【题目】已知右焦点为F(c,0)的椭圆M: ![]() =1(a>b>0)过点
=1(a>b>0)过点 ![]() ,且椭圆M关于直线x=c对称的图形过坐标原点.
,且椭圆M关于直线x=c对称的图形过坐标原点.
(1)求椭圆M的方程;
(2)过点(4,0)且不垂直于y轴的直线与椭圆M交于P,Q两点,点Q关于x轴的对称原点为E,证明:直线PE与x轴的交点为F.
【答案】
(1)解:由题意可知:椭圆M: ![]() =1(a>b>0)焦点在x轴上,
=1(a>b>0)焦点在x轴上,
椭圆过点 ![]() ,即
,即 ![]() ,
,
椭圆M关于直线x=c对称的图形过坐标原点,
∴a=2c,
由a2=b2+c2,则b2= ![]() a2,
a2,
解得:a2=4,b2=3,
∴椭圆的标准方程 ![]()
(2)证明:设直线PQ的方程为:y=k(x﹣4),k≠0,
∴ 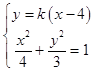 ,整理得:(3+4k2)x2﹣32k2x+64k2﹣12=0,
,整理得:(3+4k2)x2﹣32k2x+64k2﹣12=0,
∵过点P0(4,0)且不垂直于x轴的直线与椭圆交于P,Q两点,
∴由△=(﹣32k2)2﹣4(3+4k2)(64k2﹣12)>0,得:k∈(﹣ ![]() ,
, ![]() ),
),
设P(x1,y1),Q(x2,y2),E(x4,﹣y4),
则x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
则直线AE的方程为y﹣y1= ![]() (x﹣x1),
(x﹣x1),
令y=0得:x=﹣y1 ![]() +x1=
+x1= ![]() =
= 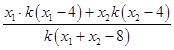 =
= ![]() =
= 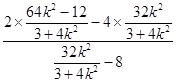 =1.
=1.
∴直线PE过定点(1,0),
由椭圆的焦点坐标为(1,0),则直线PE与x轴的交点为F
【解析】(1)由题意可知:椭圆M: ![]() =1(a>b>0)焦点在x轴上,将点
=1(a>b>0)焦点在x轴上,将点 ![]() 代入椭圆上,即
代入椭圆上,即 ![]() ,a=2c,则b2=
,a=2c,则b2= ![]() a2,即可求得a和b的值,求得椭圆方程;(2)设直线PQ的方程为:y=k(x﹣4),k≠0,代入椭圆方程,得(3+4k2)x2﹣32k2x+64k2﹣12=0,由根的判别式得到k∈(﹣
a2,即可求得a和b的值,求得椭圆方程;(2)设直线PQ的方程为:y=k(x﹣4),k≠0,代入椭圆方程,得(3+4k2)x2﹣32k2x+64k2﹣12=0,由根的判别式得到k∈(﹣ ![]() ,
, ![]() ),由韦达定理及直线的方程代入x=﹣y1
),由韦达定理及直线的方程代入x=﹣y1 ![]() +x1=1,由此能证明直线AE过定点(1,0),由椭圆的焦点坐标为(1,0),则直线PE与x轴的交点为F.
+x1=1,由此能证明直线AE过定点(1,0),由椭圆的焦点坐标为(1,0),则直线PE与x轴的交点为F.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】某学校为了调查喜欢语文学科与性别的关系,随机调查了一些学生情况,具体数据如表:
调查统计 | 不喜欢语文 | 喜欢语文 |
男 | 13 | 10 |
女 | 7 | 20 |
为了判断喜欢语文学科是否与性别有关系,根据表中的数据,得到K2的观测值k= ![]() ≈4.844,因为k≥3.841,根据下表中的参考数据:
≈4.844,因为k≥3.841,根据下表中的参考数据:
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
判定喜欢语文学科与性别有关系,那么这种判断出错的可能性为( )
A.95%
B.50%
C.25%
D.5%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的图象如图所示,为了得到函数
的图象如图所示,为了得到函数![]() 的图象,可以把函数
的图象,可以把函数![]() 的图象( )
的图象( )
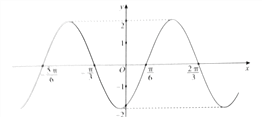
A. 每个点的横坐标缩短到原来的![]() (纵坐标不变),再向左平移
(纵坐标不变),再向左平移![]() 个单位
个单位
B. 每个点的横坐标缩短到原来的2倍(纵坐标不变),再向左平移![]() 个单位
个单位
C. 先向左平移![]() 个单位,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变)
个单位,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变)
D. 先向左平移![]() 个单位,再把所得各点的横坐标伸长到原来的
个单位,再把所得各点的横坐标伸长到原来的![]() (纵坐标不变)
(纵坐标不变)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知线段![]() 的端点
的端点![]() ,端点
,端点![]() 在圆
在圆![]() 上运动
上运动
(Ⅰ)求线段![]() 的中点
的中点![]() 的轨迹方程.
的轨迹方程.
(Ⅱ) 设动直线![]() 与圆
与圆![]() 交于
交于![]() 两点,问在
两点,问在![]() 轴正半轴上是否存在定点
轴正半轴上是否存在定点![]() ,使得直线
,使得直线![]() 与直线
与直线![]() 关于
关于![]() 轴对称?若存在,请求出点
轴对称?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体ABCD﹣A1B1C1D1中,底面ABCD是边长为 ![]() 的正方形,AA1=3,E是AA1的中点,过C1作C1F⊥平面BDE与平面ABB1A1交于点F,则
的正方形,AA1=3,E是AA1的中点,过C1作C1F⊥平面BDE与平面ABB1A1交于点F,则 ![]() =
=
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(文科)设函数f(x)=x2﹣2ax﹣8a2(a>0),记不等式f(x)≤0的解集为A.
(1)当a=1时,求集合A;
(2)若(﹣1,1)A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知线段AB的两个端点A、B分别在x轴和y轴上滑动,且∣AB∣=2.
(1)求线段AB的中点P的轨迹C的方程;
(2)求过点M(1,2)且和轨迹C相切的直线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com