

分析 由题意可以得出,图1中第n行有2n-1个数,且每行的最后一个数恰好是行号的平方,由此可以确定出ak=2017在图a中的位置,图b中每行的数字数等于行号,由此可以计算出前n行共有多少个数字,结合图a即可求出2017在图b中的位置,从而得出k的值.
解答 解:由题意,图a中第n行有2n-1个数,
前n行有n×$\frac{1+2n-1}{2}$=n×n=n2个数,
图b知各行数字个数等于行数,故前n行共有n×$\frac{1+n}{2}$=$\frac{n(n+1)}{2}$,
∵图a每行的最后一个数恰好是行号的平方,45×45=2025,
故2017是第45行倒数第9个数,
由图b知各行数字个数等于行数,故前45行共有45×$\frac{1+45}{2}$=1035,
由于最后一个数是奇数,
按图b规则知,2017是第45行倒数第5个数,故k=1035-4=1031,
故答案为:1031.
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:解答题
| 生二胎 | 不生二胎 | 合计 | |
| 70后 | 30 | 15 | 45 |
| 80后 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.25 | 0.010 | 0.005 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
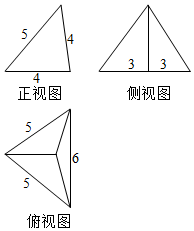
| A. | $\frac{{15\sqrt{39}}}{2}$ | B. | $\frac{{5\sqrt{39}}}{2}$ | C. | $5\sqrt{39}$ | D. | $5\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
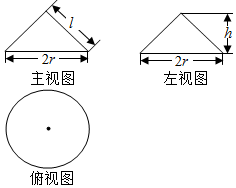
| A. | l=2r | B. | l=3r | C. | h=$\frac{{\sqrt{5}r}}{2}$ | D. | h=$\frac{{\sqrt{3}r}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com