
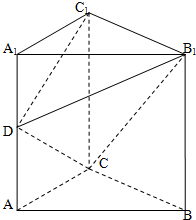
 如图在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=BC=2AC=2,D为AA1的中点.
如图在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=BC=2AC=2,D为AA1的中点.分析 (1)推导出BC⊥CC1,AC⊥BC,由此能证明CD⊥B1C1.
(2)求出D到平面B1C1C的距离d=AC=1,三棱锥C1-B1CD的体积${V}_{{C}_{1}-{B}_{1}CD}={V}_{D-{B}_{1}{C}_{1}C}$,由此能求出结果.
解答 证明:(1)∵直三棱柱ABC-A1B1C1中,CC1⊥ABC,BC?平面ABC,
∴BC⊥CC1,
∵∠ACB=90°,∴AC⊥BC,
∵AC∩CC1=C,∴BC⊥平面ACC1A1,
∵B1C1∥BC,∴B1C1⊥平面ACC1A1,
∵CD?平面ACC1A1,∴CD⊥B1C1.
解:(2)∵在直三棱柱ABC-A1B1C1中,∠ACB=90°,
AA1=BC=2AC=2,D为AA1的中点.
∴D到平面B1C1C的距离d=AC=1,
∴三棱锥C1-B1CD的体积:
${V}_{{C}_{1}-{B}_{1}CD}={V}_{D-{B}_{1}{C}_{1}C}$=$\frac{1}{3}×{S}_{△{B}_{1}{C}_{1}C}×AC$=$\frac{1}{3}×(\frac{1}{2}×2×2)×1$=$\frac{2}{3}$.
点评 本题考查线线垂直的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{7}$ | D. | $\frac{1}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≤0 | B. | m≤-1 | C. | m≥2 | D. | m≤-$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知直线l:4x+3y+15=0,半径为3的⊙C与l相切,圆心C在x轴上且在直线l的右上方.
已知直线l:4x+3y+15=0,半径为3的⊙C与l相切,圆心C在x轴上且在直线l的右上方.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(K2≥k0) | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com