
分析 (1)根据直线l的极坐标方程,求出直线的参数方程.
(2)设A,B对应的参数为t1和t2,以直线l的参数方程代入圆的方程整理得到t2+(-3-$\frac{2\sqrt{3}}{3}$)t+$\frac{13}{3}$=0,由|PA|•|PB|=|t1t2|求出点P到A、B两点的距离之积.
解答 解:(1)直线l的极坐标方程为ρsin(θ-$\frac{π}{6}$)=$\frac{\sqrt{3}-1}{2}$,直角坐标方程为y=$\frac{\sqrt{3}}{3}$x+1-$\frac{2\sqrt{3}}{3}$,
直线l的参数方程$\left\{\begin{array}{l}{x=-\sqrt{3}+tcos\frac{π}{6}}\\{y=-\frac{2\sqrt{3}}{3}+tsin\frac{π}{6}}\end{array}\right.$(t为参数);
(2)因为点A,B都在直线l上,所以可设它们对应的参数为t1和t2,
圆化为直角坐标系的方程 x2+y2=4,
以直线l的参数方程代入圆的方程整理得到 t2+(-3-$\frac{2\sqrt{3}}{3}$)t+$\frac{13}{3}$=0 ①,
因为t1和t2是方程①的解,从而 t1t2=$\frac{13}{3}$.
所以,|PA|•|PB|=|t1t2|=$\frac{13}{3}$.
点评 本题考查直线的参数方程以及参数的几何意义,极坐标方程化为直角坐标方程,利用直线的参数方程中参数的几何意义是解题的关键.


科目:高中数学 来源: 题型:选择题
| A. | (3,+∞) | B. | (0,$\frac{1}{4}$] | C. | (1,3) | D. | [$\frac{1}{4}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
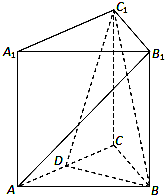 三棱ABC-A1B1C1,A1A⊥底面ABC,且△ABC为正三角形,且,D为AC中点.
三棱ABC-A1B1C1,A1A⊥底面ABC,且△ABC为正三角形,且,D为AC中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
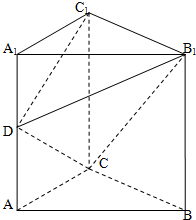 如图在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=BC=2AC=2,D为AA1的中点.
如图在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=BC=2AC=2,D为AA1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com