
 已知直线l:4x+3y+15=0,半径为3的⊙C与l相切,圆心C在x轴上且在直线l的右上方.
已知直线l:4x+3y+15=0,半径为3的⊙C与l相切,圆心C在x轴上且在直线l的右上方.分析 (1)设出圆心C坐标,根据直线l与圆C相切,得到圆心到直线l的距离d=r,确定出圆心C坐标,即可得出圆C方程;
(2)当直线AB⊥x轴,则x轴平分∠ANB,当直线AB斜率存在时,设直线AB方程为y=k(x-1),联立圆与直线方程,消去y得到关于x的一元二次方程,利用韦达定理表示出两根之和与两根之积,由若x轴平分∠ANB,则kAN=-kBN,求出t的值,确定出此时N坐标即可.
解答 解:(1)设圆心C(a,0)(a>-$\frac{15}{4}$),
∵直线l:4x+3y+15=0,半径为3的圆C与l相切,
∴d=r,即$\frac{|4a+15|}{5}$=3,
解得:a=0或a=-$\frac{15}{2}$(舍去),
则圆C方程为x2+y2=9;
(2)当直线AB⊥x轴,则x轴平分∠ANB,
若x轴平分∠ANB,则kAN=-kBN,即$\frac{k({x}_{1}-1)}{{x}_{1}-t}$+$\frac{k({x}_{2}-1)}{{x}_{2}-t}$=0,
整理得:2x1x2-(t+1)(x1+x2)+2t=0,即$\frac{2({k}^{2}-9)}{{k}^{2}+1}$-$\frac{2{k}^{2}(t+1)}{{k}^{2}+1}$+2t=0,
解得:t=9,
当点N(0,0),能使得∠ANM=∠BNM总成立.
点评 此题考查了直线与圆的方程的应用,涉及的知识有:垂径定理,勾股定理,圆的标准方程,点到直线的距离公式,以及斜率的计算,熟练掌握定理及公式是解本题的关键.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:解答题
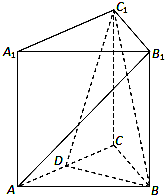 三棱ABC-A1B1C1,A1A⊥底面ABC,且△ABC为正三角形,且,D为AC中点.
三棱ABC-A1B1C1,A1A⊥底面ABC,且△ABC为正三角形,且,D为AC中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
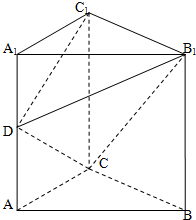 如图在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=BC=2AC=2,D为AA1的中点.
如图在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=BC=2AC=2,D为AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$ | B. | $\frac{{x}^{2}}{3}+\frac{{y}^{2}}{4}=1$ | C. | ${x}^{2}+\frac{{y}^{2}}{2}=1$ | D. | $\frac{{x}^{2}}{6}+\frac{{y}^{2}}{8}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 5 | C. | 9 | D. | -$\frac{5}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com